Cho (O) và điểm A nằm ngoài đường tròn. Vẽ cách tiếp tuyến AB, AC và cát tuyến
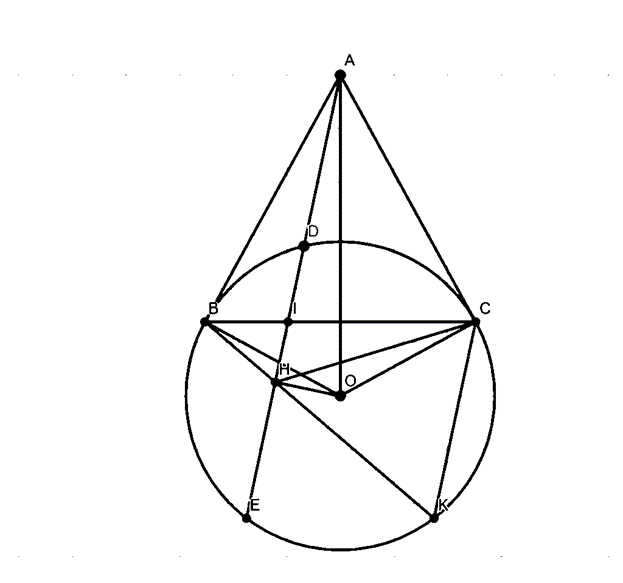
Cho (O) và điểm A nằm ngoài đường tròn. Vẽ cách tiếp tuyến AB, AC và cát tuyến ADE. Gọi H là trung điểm DE.
a) Chứng minh: A, B, H, O, C cùng nằm trên một đường tròn.
b) Chứng minh: HA là phân giác của BHC.
c) Gọi I là giao điểm của BC và DE. Chứng minh: AB2 = AI . AH.
d) BH cắt (O) ở K. Chứng minh: AE // CK.