Cho (O; R) dây MN vuông góc với OA tại trung điểm H của OA. Các tiếp tuyến với đường tròn (O) tại M và N cắt nhau ở B.

a) Chứng minh rằng 3 điểm O, A, B thẳng hàng.

b) Tam giác BMN là tam giác gì? Vì sao?

c) Tính BM theo R.

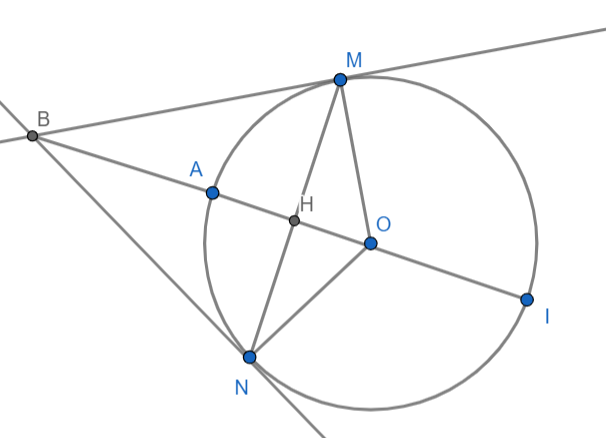
a) ΔOMA có MH⊥OA (MH là đường cao)

H là trung điểm của OA ⇒ MH là đường trung tuyến

⇒ ΔOMA cân đỉnh M.

⇒ MO = MA mà OM = OA ⇒ OM = OA = AM

⇒ ΔOMA đều

Ta có: OM = ON = R

⇒ ΔAMN cân đỉnh O có MN⊥OA = H

⇒ OH ⊥ MN

⇒ OH là đường cao 

⇒ OH cũng là phân giác của $\widehat{MON}$(1)

Xét ΔΔ vuông MOB và ΔΔ vuông NOB ta có:

OB chung

OM = ON = R

⇒ ΔMOB = ΔNOB (cạnh huyền – cạnh góc vuông)

⇒ $\widehat{MOB}=\widehat{NOB}$

⇒ OB là phân giác $\widehat{MON}$  (2)

Từ (1) và (2) ⇒ OA, OB cùng là phân giác $\widehat{MON}$

⇒ O, A, B thẳng hàng.

b) OA ⊥ MN và OH ∩ MN = H là trung điểm MN

⇒ ΔBMN có BH ⊥ MN; BH là đường cao và BH là đường trung tuyến

⇒ ΔBMN cân đỉnh B.

⇒ $\widehat{MBO}=90°-\widehat{MOA}=90°-60°=30°$

Suy ra: $\widehat{MBN}=2.\widehat{MBO}=60°$

⇒ΔMBN là tam giác đều.

c) MB = MN = 2MH

Áp dụng định lý Pitago vào Δ vuông MOH ta có:

MH² = AM² – OH² = R² − ${\left(\frac{R}{2}\right)}^2$

⇒ MH = $\frac{R\sqrt{3}}{2}$

⇒ MB = MN = 2MH = $R\sqrt{3}$