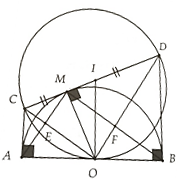
Cho nửa đường tròn tâm O đường kính AB và M là điểm nằm trên (O). Tiếp tuyến tại M cắt tiếp tuyến tại A và B của (O) lần lượt ở C và D. Đường thẳng AM cắt OC tại E, đường thẳng BM cắt OD tại F

a, Chứng minh: $\widehat{COD}$  = 90°.

b, Tứ giác MEOF là hình gì?

c, Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.

a, Dễ thấy $\widehat{AMB}$ = 90° hay $\widehat{EMF}$   = 90° (  là góc nội tiếp chắn nửa đường tròn)

Tiếp tuyến CM, CA ⇒ OC ⊥ AM ⇒ $\widehat{OEM}$  = 90° 

Tương tự ⇒ $\widehat{OEM}$ = 90° 

Xét ∆CAO và ∆CMO có:

CM = CA (tính chất 2 tiếp tuyến cắt nhau)

 $\widehat{CMO}=\widehat{CAO}$= 90° 

Chung CO

⇒ ∆CAO = ∆CMO (c.g.c)

⇒  $\widehat{AOC}=\widehat{MOC}$

⇒ OC là tia phân giác của $\widehat{AMO}$

Tương tự OD là tia phân giác của $\widehat{BOM}$  suy ra OC ⊥ OD ⇒ $\widehat{COD}$  = 90°

b, Do ∆AOM cân tại O nên OE là đường phân giác đồng thời là đường cao

⇒ $\widehat{OEM}$   = 90°chứng minh tương tự  = 90° 

Vậy MEOF là hình chữ nhật.

c, Gọi I là trung điểm CD thì I là tâm đường tròn đường kính CD và IO = IC = ID.

Có ABDC là hình thang vuông tại A và B nên IO // AC // BD và IO vuông góc với AB.

Do đó AB là tiếp tuyến của đường tròn đường kính CD.