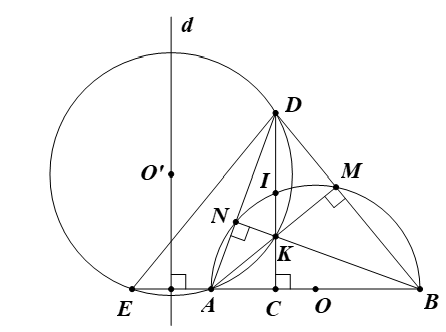
Cho nửa đường tròn tâm O đường kính AB, C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I, K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I). Tia AK cắt nửa đường tròn tâm O tại M, tia BM cắt tia CI tại D. Chứng minh:

a) Các tứ giác ACMD, BCKM nội tiếp đường tròn.

a)

Ta có $\widehat{ACD}=90°$  (CD ⊥ AB tại C).

Suy ra ba điểm A, C, D cùng thuộc đường tròn đường kính AD (1)

Ta có  $\widehat{AMB}=90°$(góc nội tiếp chắn nửa đường tròn (O)).

Hay$\widehat{AMD}=90°$ .

Suy ra ba điểm A, M, D cùng thuộc đường tròn đường kính AD (2)

Từ (1), (2), ta suy ra tứ giác ACMD nội tiếp đường tròn đường kính AD.

Ta có $\widehat{BCK}=90°$   (CD ⊥ AB tại C).

Suy ra ba điểm B, C, K cùng thuộc đường tròn đường kính BK (3)

Ta có $\widehat{KMB}=90°$  (góc nội tiếp chắn nửa đường tròn (O)).

Suy ra ba điểm K, M, B cùng thuộc đường tròn đường kính BK (4)

Từ (3), (4), ta suy ra tứ giác BCKM nội tiếp đường tròn đường kính BK.