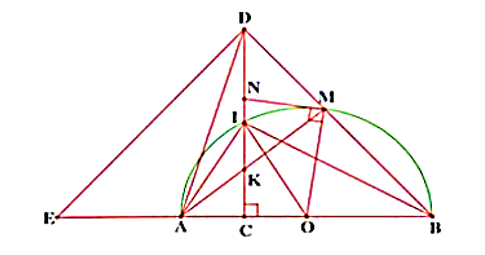
Cho nửa đường tròn tâm O đường kính AB = 2R. Gọi C là trung điểm OA, tia Cx vuông góc AB, Cx cắt nửa đường tròn (O) tại I. Lấy K là 1 điểm bất kì trên CI (K khác C và I). AK cắt nửa đường trò
Cho nửa đường tròn tâm O đường kính AB = 2R. Gọi C là trung điểm OA, tia Cx vuông góc AB, Cx cắt nửa đường tròn (O) tại I. Lấy K là 1 điểm bất kì trên CI (K khác C và I). AK cắt nửa đường tròn (O) tại M. Tiếp tuyến với (O) tại M cắt Cx tại N. BM cắt Cx tại D.
a) Chứng minh: 4 điểm A, C, M, D thuộc 1 đường tròn.