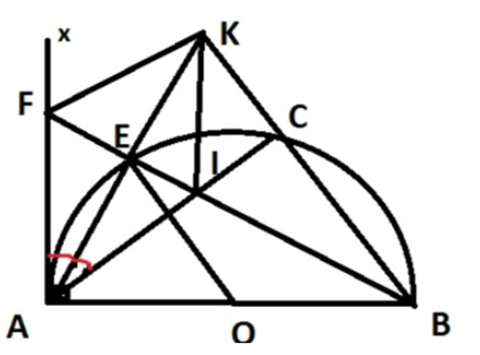
Cho nửa đường tròn (O) đường kính AB, tiếp tuyến Ax. Gọi C là một điểm trên nửa
Cho nửa đường tròn (O) đường kính AB, tiếp tuyến Ax. Gọi C là một điểm trên nửa đường tròn. Tia phân giác của \(\widehat {CAx}\) cắt nửa đường tròn ở E, AE và BC cắt nhau ở K. AC cắt BE ở I.
a) Tam giác ABK là tam giác gì? Vì sao?
b) Chứng minh KI // Ax.
c) Chứng minh OE // BC.