Bài 11 trang 70 SBT Toán 7 Tập 2: Cho năm điểm A, B, C, D, E cùng nằm trên một đường thẳng d sao cho AB = DE, BC = CD. Điểm M không thuộc d sao cho MC vuông góc với d. Chứng minh rằng:
a) ΔMBC = ΔMDC và ΔMAC = ΔMEC.
b) ΔMAB = ΔMED.
Lời giải:
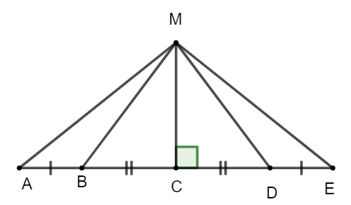
a) Xét ΔMBC và ΔMDC cùng vuông tại C có :
BC = CD (gt);
MC là cạnh chung.
Do đó ΔMBC = ΔMDC (hai cạnh góc vuông).
Ta có: CA = BC + AB
CE = CD + DE
Mà AB = DE (gt); BC = CD (gt)
Do đó CA = CE
Xét ΔMAC và ΔMEC cùng vuông tại C có :
CA = CE (cmt);
MC là cạnh chung.
Do đó ΔMAC = ΔMEC (hai cạnh góc vuông).
b) Xét ΔMAB và ΔMED có :
AB = ED ( gt);
MA = ME (ΔMAC = ΔMEC, hai cạnh tương ứng);
góc MAB = góc MED (ΔMAC = ΔMEC)
Do đó ΔMAB = ΔMED (c.g.c).
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
Bài 36: Hình hộp chữ nhật và hình lập phương
Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác