Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
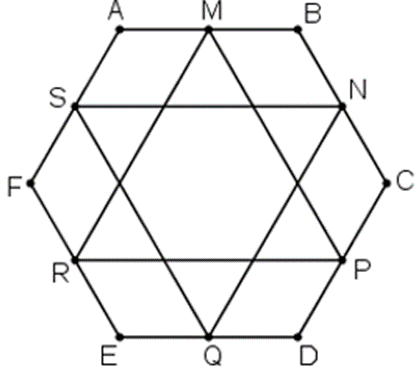
Gọi G là trọng tâm tam giác MPR ⇒ \(\overrightarrow {GM} + \overrightarrow {GP} + \overrightarrow {GR} = \overrightarrow 0 \)
Ta cần đi chứng minh G cũng là trọng tâm của ΔNQS bằng cách chứng minh \(\overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GS} = \overrightarrow 0 \)
Thật vậy ta có:
\(2\left( {\overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GS} } \right) = 2\overrightarrow {GN} + 2\overrightarrow {GQ} + 2\overrightarrow {GS} \)
\( = \left( {\overrightarrow {GB} + \overrightarrow {GC} } \right) + \left( {\overrightarrow {GD} + \overrightarrow {GE} } \right) + \left( {\overrightarrow {GF} + \overrightarrow {GA} } \right)\) (Vì N, Q, S là trung diểm BC, DE, FA)
\( = \left( {\overrightarrow {GA} + \overrightarrow {GB} } \right) + \left( {\overrightarrow {GC} + \overrightarrow {GD} } \right) + \left( {\overrightarrow {GE} + \overrightarrow {GF} } \right)\)
\( = 2\overrightarrow {GM} + 2\overrightarrow {GP} + 2\overrightarrow {GR} \) (Vì M, P, R là trung diểm AB, CD, EF)
\( = 2\left( {\overrightarrow {GM} + \overrightarrow {GP} + \overrightarrow {GR} } \right) = \overrightarrow 0 \)
Suy ra: \(\overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GS} = \overrightarrow 0 \) hay G cũng là trọng tâm của ΔNQS.
Vậy trọng tâm ΔMPR và ΔNQS trùng nhau.