Cho lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác vuông tại A. E là trung
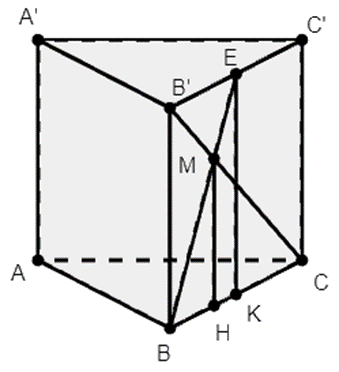
Cho lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác vuông tại A. E là trung điểm của B’C’, CB’ cắt BE tại M. Tính thể tích V của khối tứ diện ABCM biết AB = 3a, AA’ = 6a.
A. V = 6a3;
B. \[V = 6\sqrt 2 {a^3}\];
C. V = 8a3;
D. V = 7a3.