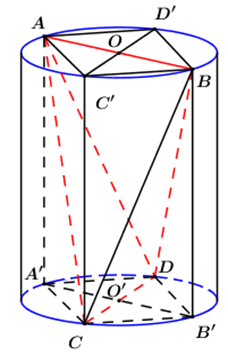
Gọi A', B' lần lượt là hình chiếu của A, B lên đường tròn (O).
C', D' lần lượt là hình chiếu của C, D lên đường tròn (O').
Suy ra AC'BD' là hình bình hành, lại có AB = CD = C'D' nên AC'BD' là hình chữ nhật.
Khi đó AC'BD'.A'CB'D là hình hộp chữ nhật.
Ta có: VAC'BD'.A'CB'D = VA.BCD + VA.A'CD + VB.B'CD + VC.C'AB + VD.D'AB
\({V_{A.A'CD}} = \frac{1}{3}AA'\,.\,{S_{A'CD}} = \frac{1}{3}AA'\,.\,\frac{1}{2}{S_{A'CB'D}} = \frac{1}{6}{V_{AC'BD'.A'CB'D}}\)
Chứng minh tương tự ta có: \({V_{B.B'CD}} = {V_{C.C'AB}} = {V_{D.D'AB}} = \frac{1}{6}{V_{AC'BD'.A'CB'D}}\)
\[ \Rightarrow {V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + 4\,.\,\frac{1}{6}{V_{AC'BD'.A'CB'D}}\]
\[ \Rightarrow {V_{ABCD}} = \frac{1}{3}{V_{AC'BD'.A'CB'D}} = 30\]
Þ VAC'BD'.A'CB'D = 90.
Theo bài ra ta có: \(\left( {\widehat {AB;\;CD}} \right) = 30^\circ \Rightarrow \left( {\widehat {AB;\;C'D'}} \right) = 30^\circ \).
Giả sử \(\left( {\widehat {AB;\;C'D'}} \right) = \widehat {AOC'} = 30^\circ \).
Lại có: \[OA = OC' = \frac{1}{2}AB = 3\]
\( \Rightarrow {S_{OAC'}} = \frac{1}{2}OA\,.\,OC'\,.\,\sin \widehat {AOC'} = \frac{1}{2}\,.\,3\,.\,3\,.\,\sin 30^\circ = \frac{9}{4}\)
Þ SAC'BD' = 4SOAC' = 9.
Ta có: VAC'BD'.A'CB'D = AA'.SAC'BD'
Þ 90 = AA'.9 Û AA' = 10.
Vậy thể tích khối trụ là:
V = pr2h = p.OA2.AA' = p.32.10 = 90p.