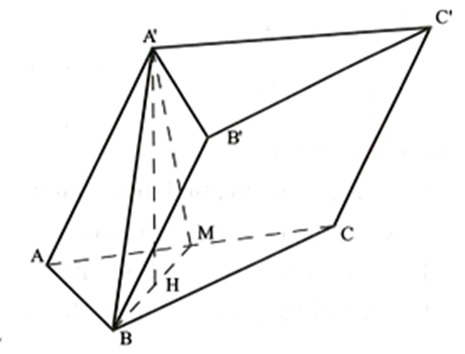
Gọi H là trung điểm BM, tam giác A'BM cân tại A' nên A'H ^ BM

Ta có: 

\(\left\{ \begin{array}{l}\left( {A'BM} \right) \bot \left( {ABC} \right)\\\left( {A'BM} \right) \cap \left( {ABC} \right) = BM\\A'H \bot BM\end{array} \right. \Rightarrow A'H \bot \left( {ABC} \right)\)

Tam giác ABC đều cạnh a nên ta có: 

\(\left\{ \begin{array}{l}BM = \frac{{a\sqrt 3 }}{2} \Rightarrow BH = \frac{{a\sqrt 3 }}{4}\\{S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\end{array} \right.\)

A'B có hình chiếu vuông góc trên (ABC) là HB

Góc tạo bởi A'B với mặt phẳng (ABC) là góc A'BH (vì góc A'BH là góc nhọn)

Xét tam giác A'BH vuông tại H, ta có: \(\widehat {A'BH} = 30^\circ \)

\(\tan \widehat {A'BH} = \frac{{A'H}}{{BH}}\)

\( \Rightarrow \tan 30^\circ = \frac{{A'H}}{{\frac{{a\sqrt 3 }}{4}}}\)

\( \Rightarrow A'H = \frac{{a\sqrt 3 }}{4}\,.\,\tan 30^\circ = \frac{a}{4}\)

Vậy \({V_{ABC.A'B'C'}} = A'H\,.\,{S_{\Delta ABC}} = \frac{a}{4}\,.\,\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{{16}}\).