Cho khối chóp đều S.ABCD có tất cả các cạnh đều bằng a căn bậc hai của 3. Tính thể tích V của khối cầu ngoại tiếp hình chóp.
Cho khối chóp đều S.ABCD có tất cả các cạnh đều bằng \(a\sqrt 3 \). Tính thể tích V của khối cầu ngoại tiếp hình chóp.
Lời giải
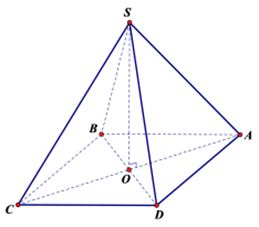
Gọi O là giao điểm của AC và BD ta có OA = OB = OC = OD
Ta lại có DABC = DASC Þ BO = SO
Þ OA = OB = OC = OD = SO
Suy ra O là tâm của khối cầu ngoại tiếp hình chóp S.ABCD
Ta có \(r = OA = \frac{{a\sqrt 3 \,.\,\sqrt 2 }}{2} = \frac{{a\sqrt 6 }}{2}\)
Vậy, \(V = \frac{4}{3}\pi {\left( {\frac{{a\sqrt 6 }}{2}} \right)^3} = \pi {a^3}\sqrt 6 \)