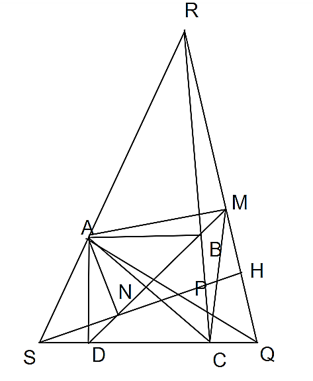
Cho hình vuông ABCD. Qua A vẽ 2 đường thẳng vuông góc với nhau, cắt BC tại Q và R, cắt CD tại P và S.

a) Tam giác AQR và APS là tam giác cân.

a) Xét tam giác vuông ABR và ADQ có:

AB = AD (giả thiết)

$\widehat{BAR}+\widehat{BAP}$= 90°

$\widehat{DAQ}+\widehat{BAP}$Góc = 90°

⇒   $\widehat{BAR}=\widehat{DAQ}$

⇒ ∆ABR = ∆ADQ (cạnh góc vuông – góc nhọn kề)

⇒ AR = AQ (2 cạnh tương ứng)

⇒ Tam giác AQR cân tại A.

Chứng minh tương tự: ta có ∆ADS = ∆ABP

⇒ AS = AP ⇒ ∆APS cân tại A.