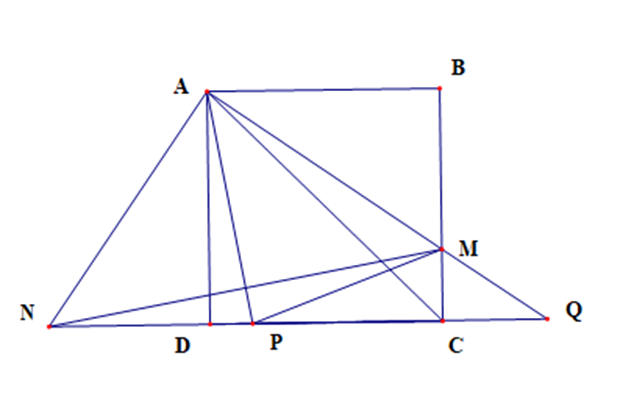
a) Vì ABCD là hình vuông nên AB = BC = CD = DA và \(\widehat {ABC} = \widehat {BC{\rm{D}}} = \widehat {C{\rm{D}}A} = \widehat {DAB} = 90^\circ \)

Ta có:

\(\widehat {MAN} = \widehat {MA{\rm{D}}} + \widehat {DAN} = 90^\circ \)

\(\widehat {BA{\rm{D}}} = \widehat {MA{\rm{D}}} + \widehat {MAB} = 90^\circ \)

Suy ra \(\widehat {DAN} = \widehat {BAM}\)

Xét tam giác ADN và tam giác ABM có

\(\widehat {A{\rm{D}}N} = \widehat {ABM}\left( { = 90^\circ } \right)\)

AD = AB (chứng minh trên)

\(\widehat {DAN} = \widehat {BAM}\) (chứng minh trên)

Suy ra ∆ADN = ∆ABM (g.c.g)

Do đó AM = AN, DN = BM (các cặp cạnh tương ứng)

Suy ra tam giác AMN cân tại A

Khi đó tam giác AMN vuông cân tại A

Xét tam giác AMN cân tại A có AP là đường cao nên AP đồng thời là phân giác

Do đó \(\widehat {NAP} = \widehat {MAP} = \frac{1}{2}\widehat {MAN} = \frac{1}{2}.90^\circ = 45^\circ \)

Vì ABCD là hình vuông có CA là đường chéo nên \(\widehat {AC{\rm{D}}} = \widehat {ACB} = \frac{{90^\circ }}{2} = 45^\circ \)

Xét ∆ACN và ∆PAN có

\(\widehat {NAP} = \widehat {NCA}\left( { = 45^\circ } \right)\)

\(\widehat {ANC}\) là góc chung

Suy ra (g.g)

Do đó \(\frac{{AN}}{{PN}} = \frac{{CN}}{{AN}}\)

Hay AN² = NC . NP

b) Xét tam giác APN và tam giác APM có

AP là cạnh chung

\(\widehat {PAN} = \widehat {PAM}\) (chứng minh câu a)

AN = AM (chứng minh câu a)

Suy ra ∆APN = ∆APM (c.g.c)

Do đó PM = PN (hai cạnh tương ứng)

Chu vi tam giác MCP là:

CM + MP + CP = CM + PN + CP = CM + PB + DN + CP

= CM + PB + BM + CP = (CM + BM) + (PB + CP) = CD + CB = 2BC

Chu vi hình vuông ABCD là: 4BC

Vậy tỉ số chu vi tam giác CMP và chu vi hình vuông ABCD bằng \(\frac{{2BC}}{{4BC}} = \frac{1}{2}\)

c) Ta có: \[{{\rm{S}}_{ANQ}} = \frac{1}{2}AN.AQ = \frac{1}{2}A{\rm{D}}.NQ\]

Suy ra \(\frac{1}{{A{\rm{D}}}} = \frac{{NQ}}{{AN.AQ}}\)

Do đó \(\frac{1}{{A{{\rm{D}}^2}}} = \frac{{N{Q^2}}}{{A{N^2}.A{Q^2}}}\)

Vì tam giác ANQ vuông tại A nên AN² + AQ² = NQ²

Suy ra \(\frac{1}{{A{{\rm{D}}^2}}} = \frac{{A{N^2} + A{Q^2}}}{{A{N^2}.A{Q^2}}} = \frac{1}{{A{N^2}}} + \frac{1}{{A{Q^2}}}\)

Vì AD là cạnh hình vuông nên AD không đổi

Suy ra tổng \(\frac{1}{{A{M^2}}} + \frac{1}{{A{Q^2}}}\) không đổi khi điểm M thay đổi trên cạnh BC

Vậy tổng \(\frac{1}{{A{M^2}}} + \frac{1}{{A{Q^2}}}\) không đổi khi điểm M thay đổi trên cạnh BC.