Câu hỏi:
25/01/2024 82Cho hình vẽ dưới đây. Khẳng định đúng là
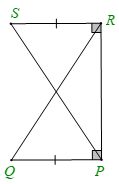
A. ΔSRP=ΔQPR;
B. ΔSRP=ΔQRP;
C. ΔRSP=ΔPRQ;
D. ΔPRS=ΔPQR.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
Hai tam giác SRP (vuông tại R) và tam giác QPR (vuông tại P) có:
RP là cạnh chung
SR = QP
Nên ΔSRP=ΔQPR (hai cạnh góc vuông).
(Đỉnh S tương ứng với đỉnh Q; đỉnh R của tam giác này tương ứng với đỉnh P của tam giác kia và ngược lại).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC vuông tại A, BD là tia phân giác của góc ABC và BA = BE (E thuộc BC). Số đo góc BED là
Câu 2:
Cho tam giác ABC có M là trung điểm cạnh BC. Kẻ tia Ax đi qua M. Qua B, C lần lượt kẻ các đường thẳng vuông góc với Ax, cắt Ax tại H, K. So sánh BH và CK.
Câu 3:
Cho tam giác ABC có AB = AC . Trên cạnh AB và AC lấy các điểm D, E sao cho AD = AE. Gọi K là giao điểm của BE và CD. Chọn câu sai.
Câu 4:
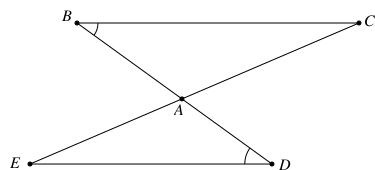
Cho hình vẽ. Với các kí hiệu trên hình vẽ, cần thêm yếu tố nào để ΔABC=ΔADE (g.c.g)
Câu 6:
Cho tam giác ABC vuông tại A và tam giác POI vuông tại I có BC = OP, ˆC=ˆP. Khẳng định đúng là
Câu 10:
Cho M, N là hai điểm phân biệt nằm trên đường trung trực của cạnh AB sao cho AM = BN. O là giao điểm của MN và AB. Khẳng định sai là
Câu 11:
Tổng ba góc ngoài (mỗi đỉnh của tam giác ta chỉ lấy một góc) của một tam giác bằng:
Câu 12:
Cho ΔABC (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng một tam giác có ba đỉnh là H, I, K. Viết kí hiệu về sự bằng nhau của hai tam giác, biết rằng AB = IK, BC = KH.