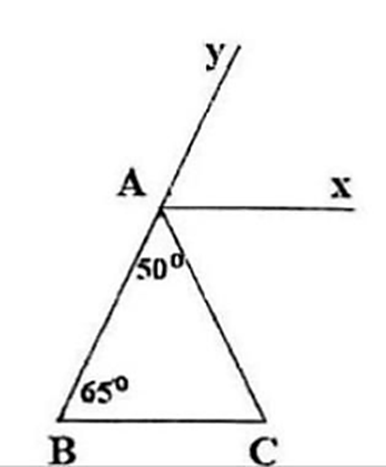
a) Xét tam giác ABC có:
\(\widehat {BAC} + \widehat {ABC} + \widehat {ACB}\) = 180°
⇔ 50° + 65° + \(\widehat {ACB}\)= 180°
⇔ \(\widehat {ACB}\)= 65°
b) Do Ax // BC nên \(\widehat {ACB} = \widehat {CAx} = 65^\circ \)(so le trong)
Suy ra: \(\widehat {BAx} = 50^\circ + 65^\circ = 115^\circ \)
Ta có: \(\widehat {BAx} + \widehat {yAx} = 180^\circ \)
⇔ \(\widehat {yAx} = 180^\circ - 115^\circ = 65^\circ \)
Suy ra: \(\widehat {yAx} = \widehat {CAx} = 65^\circ \)nên Ax là tia phân giác \(\widehat {yAC}\)
c) Do Az là tia đối của Ax nên \(\widehat {xAz} = 180^\circ \)
Lại có: \(\widehat {xAz} = \widehat {BAx} + \widehat {BAz}\)
Suy ra: \(\widehat {BAz} = 180^\circ - 115^\circ = 65^\circ \)
Do Am là phân giác của \(\widehat {BAz}\)
nên \[\widehat {BAm} = \frac{1}{2}\widehat {BAz} = \frac{1}{2}.65^\circ = 32,5^\circ \]
Mặt khác: Bn là phân giác của \(\widehat {ABC}\)
nên \[\widehat {ABn} = \frac{1}{2}\widehat {ABC} = \frac{1}{2}.65^\circ = 32,5^\circ \]
Do đó: \[\widehat {BAm} = \widehat {ABn}\]mà 2 góc này ở vị trí so le trong
Nên Am // Bn.