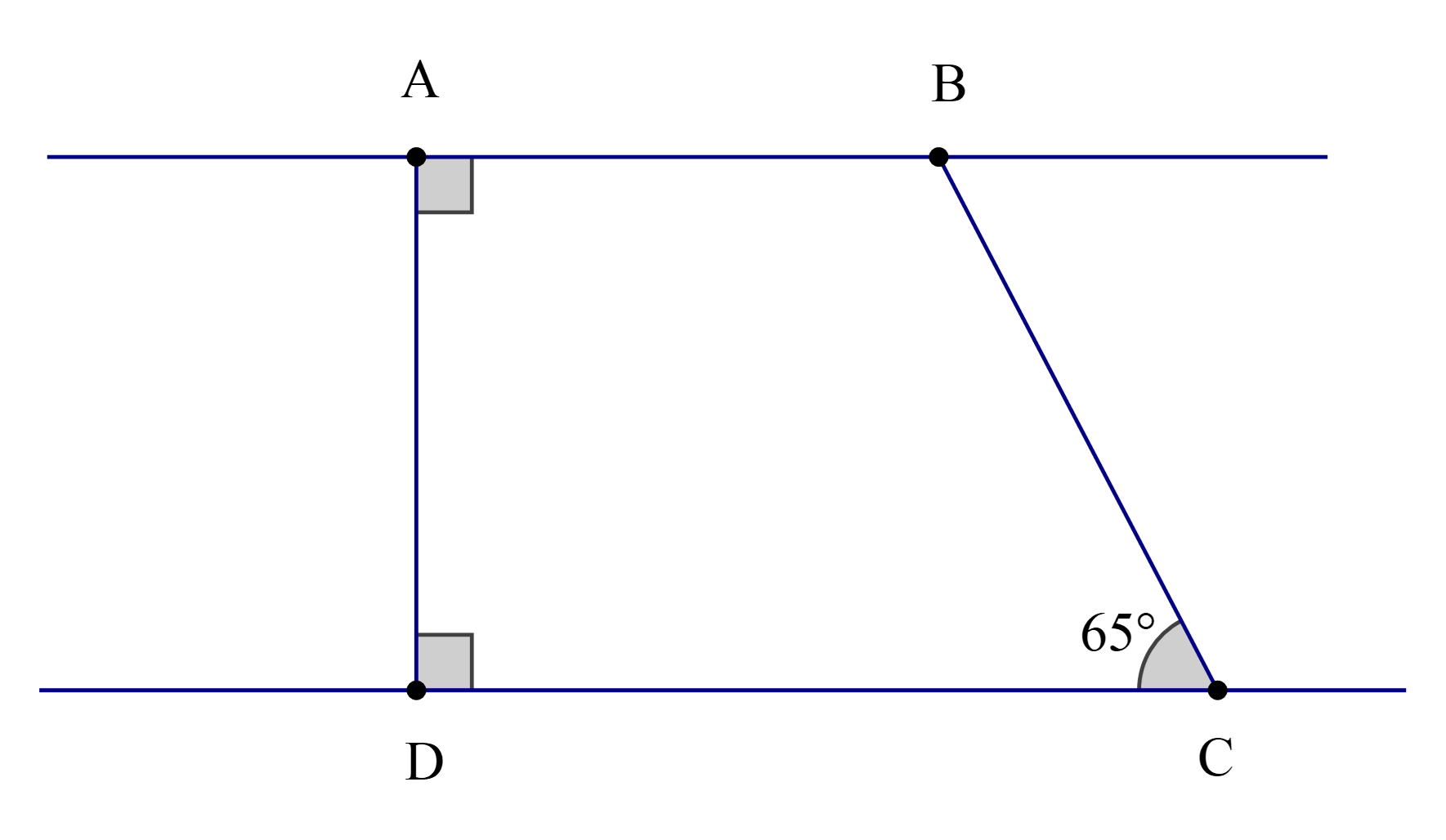
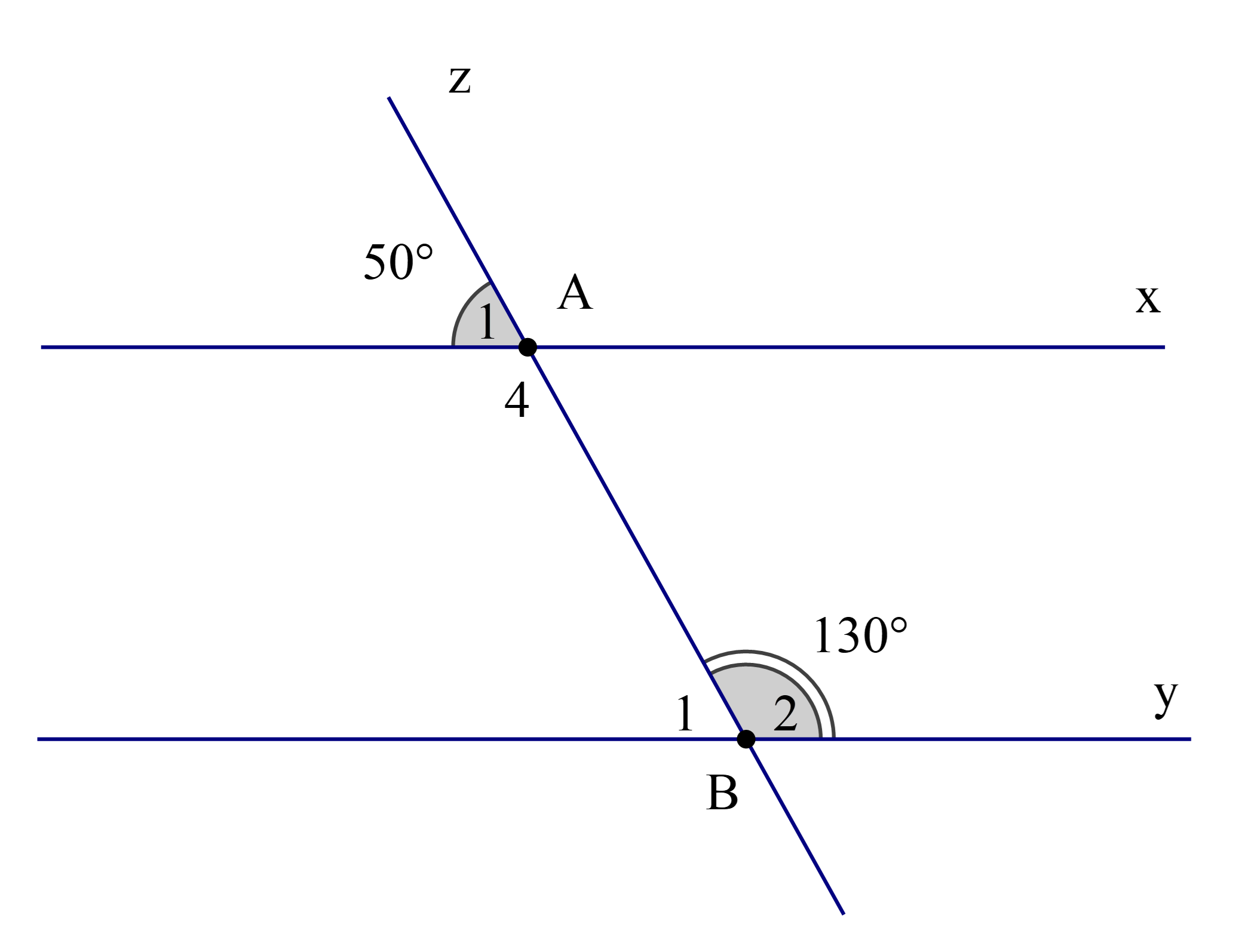
Câu hỏi:
01/02/2024 72Cho hình vẽ
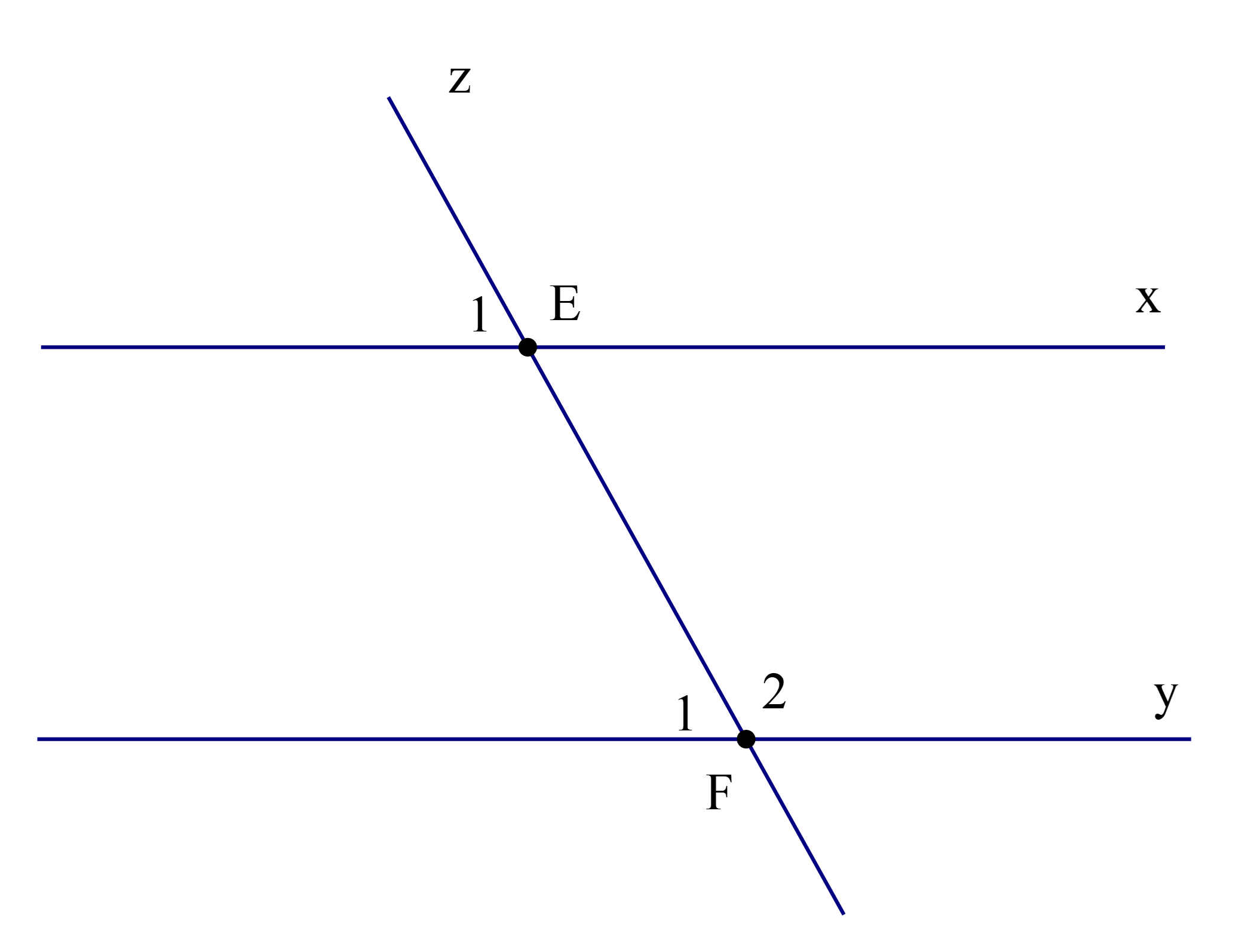
Biết rằng x // y và ˆF2=2ˆF1. Số đo của ˆE1 là:
A. 30°;
B. 45°;
C. 55°;
D. 60°.
Đáp án chính xác
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Ta có ˆF1+ˆF2=180∘ (hai góc kề bù) (1)
Mà ˆF2=2ˆF1 (giả thiết) (2)
Từ (1) và (2) suy ra ˆF1+2ˆF1=180∘
Hay 3ˆF1=180∘
Suy ra ˆF1=180∘3=60∘
Theo bài ta có x // y
Do đó ˆE1=ˆF1=60∘ (hai góc đồng vị)
Vậy ta chọn phương án D.
Hướng dẫn giải
Đáp án đúng là: D
Ta có ˆF1+ˆF2=180∘ (hai góc kề bù) (1)
Mà ˆF2=2ˆF1 (giả thiết) (2)
Từ (1) và (2) suy ra ˆF1+2ˆF1=180∘
Hay 3ˆF1=180∘
Suy ra ˆF1=180∘3=60∘
Theo bài ta có x // y
Do đó ˆE1=ˆF1=60∘ (hai góc đồng vị)
Vậy ta chọn phương án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Cho hình vẽ
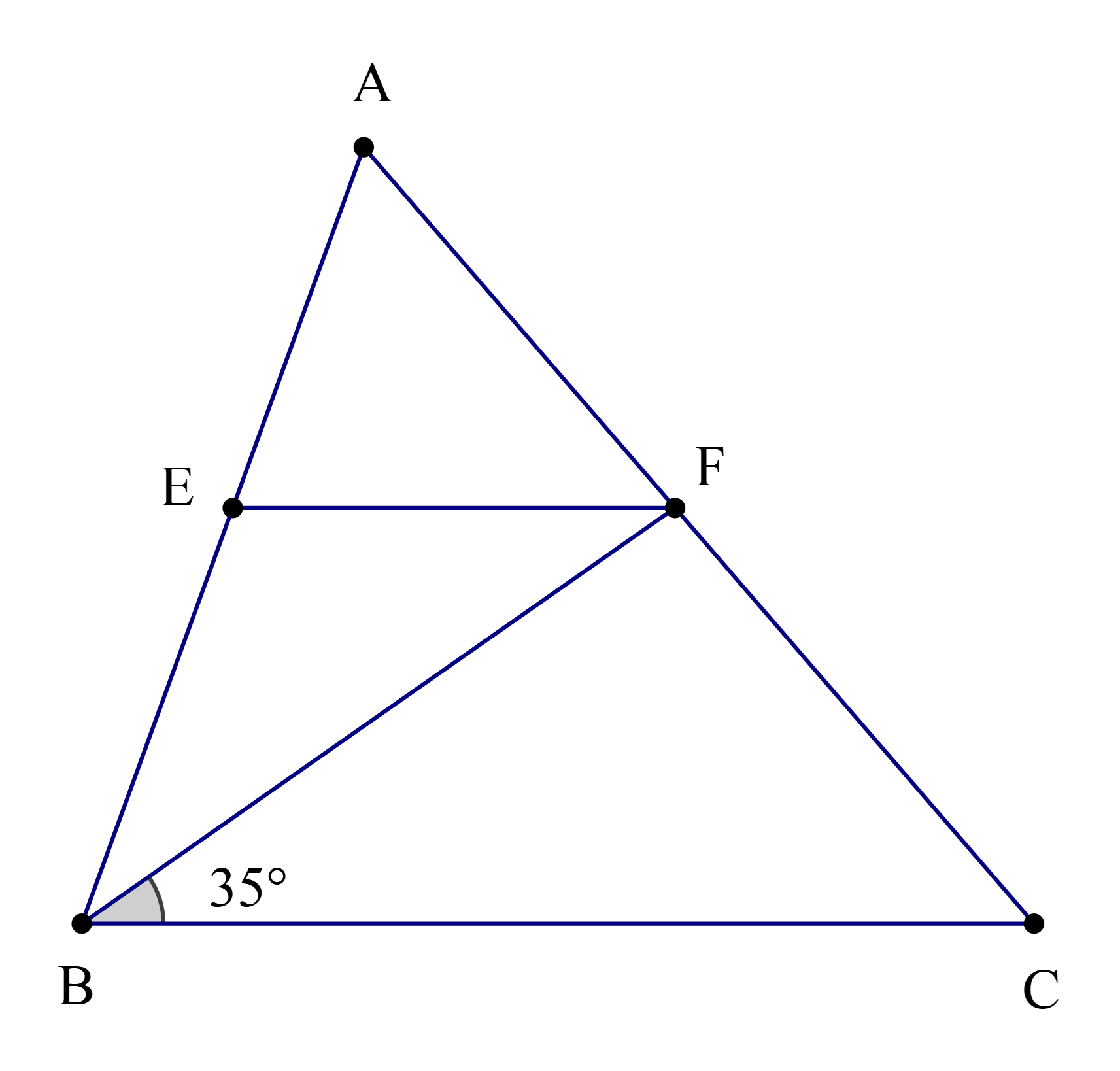
Biết rằng BF là phân giác của ^ABC, EF // BC và ^FBC=35∘. Số đo của ^AEF là:
Xem đáp án »
01/02/2024
73
Câu 4:
Cho hình vẽ

Biết rằng BF là phân giác của ^ABC, EF // BC và ^FBC=35∘. Số đo của ^AEF là:
Xem đáp án »
01/02/2024
73
Câu 5:
Cho hình vẽ. Biết rằng x // y; đường thẳng z cắt hai đường thẳng x, y lần lượt tại A, B sao cho ˆA1=60∘.
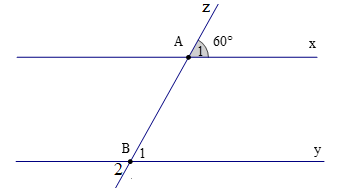
Số đó của ˆB2 là:
Xem đáp án »
01/02/2024
69
Câu 6:
Cho hình vẽ
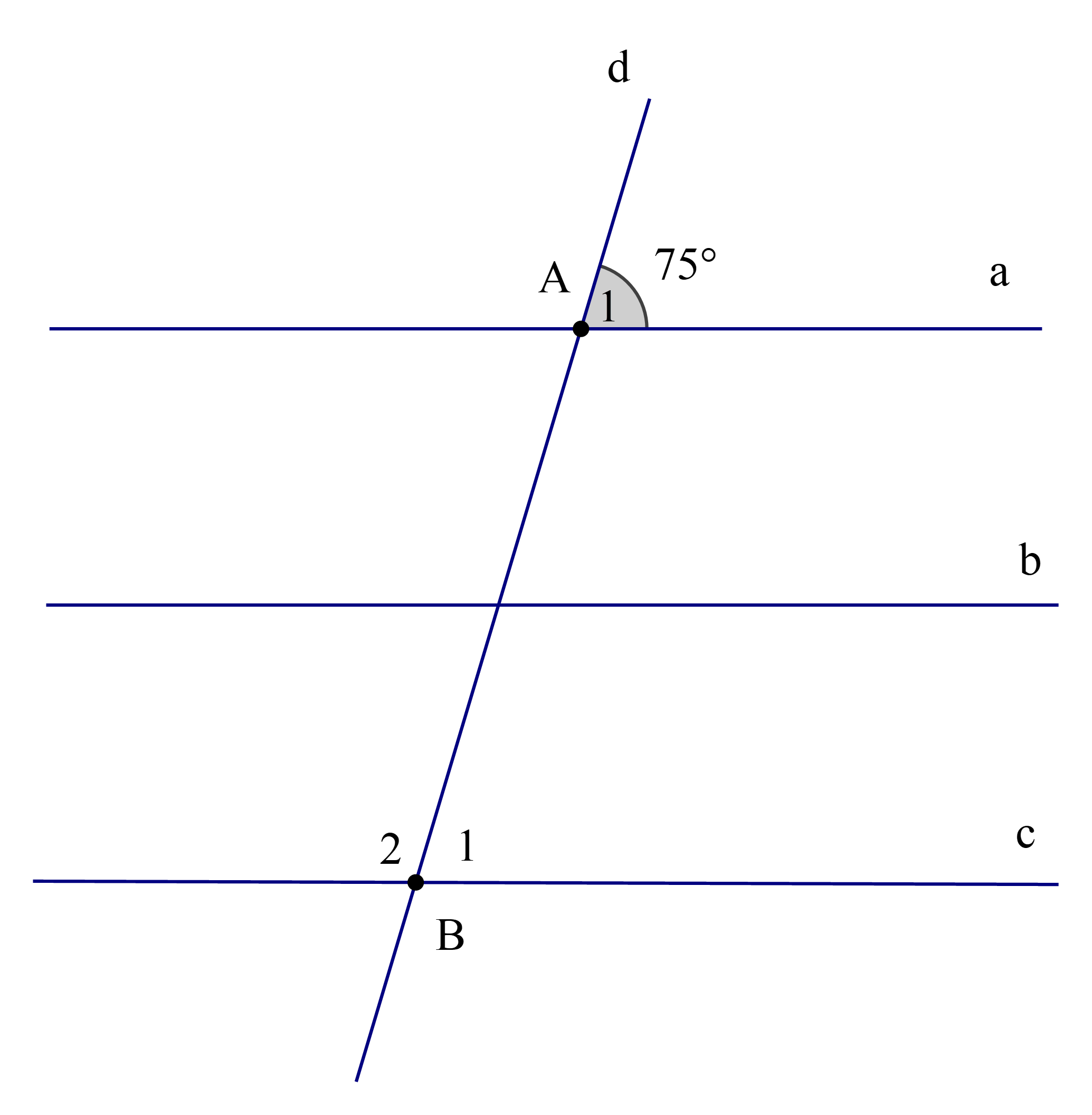
Biết rằng a // b; b // c và ˆA1=75∘. Số đo của ˆB2 là:
Xem đáp án »
01/02/2024
69