Câu hỏi:
25/01/2024 47
Cho hình vẽ bên.
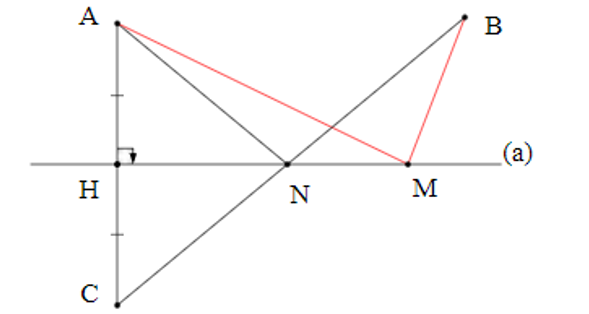
Vị trí của điểm M trên đường thẳng (a) để MA + MB nhỏ nhất là:
Cho hình vẽ bên.

Vị trí của điểm M trên đường thẳng (a) để MA + MB nhỏ nhất là:
A. M trùng N;
A. M trùng N;
B. M là điểm bất kì trên đường thẳng (a);
B. M là điểm bất kì trên đường thẳng (a);
C. M trùng H;
D. Không có điểm M nào thỏa mãn yêu cầu bài toán.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Ta có (a) đi qua trung điểm H của đoạn thẳng AC và vuông góc với AC tại H.
Suy ra (a) là đường trung trực của đoạn thẳng AC.
Vì M ∈ (a) nên M cách đều A và C. Tức là, MA = MC.
Ta có MA + MB = MC + MB ≥ BC.
Vì vậy MA + MC nhỏ nhất khi và chỉ khi MA + MC = BC.
Tức là M là giao điểm của (a) và BC.
Khi đó M trùng N.
Vậy ta chọn phương án A.
Hướng dẫn giải
Đáp án đúng là: A
Ta có (a) đi qua trung điểm H của đoạn thẳng AC và vuông góc với AC tại H.
Suy ra (a) là đường trung trực của đoạn thẳng AC.
Vì M ∈ (a) nên M cách đều A và C. Tức là, MA = MC.
Ta có MA + MB = MC + MB ≥ BC.
Vì vậy MA + MC nhỏ nhất khi và chỉ khi MA + MC = BC.
Tức là M là giao điểm của (a) và BC.
Khi đó M trùng N.
Vậy ta chọn phương án A.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆MAB, ∆NAB, ∆PAB là tam giác cân chung đáy AB. Kết luận nào sau đây sai?
Cho ∆MAB, ∆NAB, ∆PAB là tam giác cân chung đáy AB. Kết luận nào sau đây sai?
Câu 2:
Cho tam giác ABC cân tại A. Từ BE và CF lần lượt vuông góc với AC và AB (E ∈ AC, F ∈ AB). Gọi H là giao điểm của BE và CF, D là trung điểm của BC.
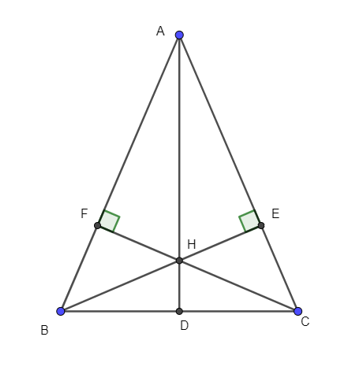
Cho tam giác ABC cân tại A. Từ BE và CF lần lượt vuông góc với AC và AB (E ∈ AC, F ∈ AB). Gọi H là giao điểm của BE và CF, D là trung điểm của BC.



