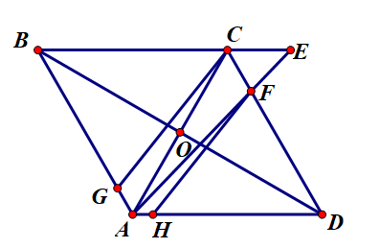
Cho hình thoi ABCD có  $\widehat{ABC}=60°$. Hai đường chéo cắt nhau tại O, E thuộc tia BC sao cho  $BE=\frac{4}{3}BC$, AE cắt CD tại F. Trên hai đoạn AB và AD lần lượt lấy hai điểm G và H sao cho CG song song với FH.

Chứng minh rằng:  $BG.DH=\frac{3}{4}B{C}^2$.

Do ABCD là hình thoi suy ra BC // AD hay CB // HD

Mà CG // HF (gt) nên suy ra  $\widehat{BCG}=\widehat{DHF}$

Ta có ABCD là hình thoi nên suy ra  $\widehat{CBG}=\widehat{HDF}$

Xét DBCG và DDHF có:

 $\widehat{BCG}=\widehat{DHF}$ (cmt)

 $\widehat{CBG}=\widehat{HDF}$ (cmt)

Suy ra DBCG ᔕ DDHF (g.g)

 $\Rightarrow \frac{BC}{DH}=\frac{BG}{DF}\Rightarrow BG.DH=BC.DF$ (1)

Lại có:   $BE=\frac{4}{3}BC\Rightarrow \frac{BC}{BE}=\frac{3}{4}\Rightarrow \frac{CE}{BC}=\frac{1}{3}\Rightarrow \frac{CE}{AD}=\frac{1}{3}$ 

Với CE // AD nên theo định lý Ta-lét thì:

 $\frac{CF}{DF}=\frac{CE}{AD}=\frac{1}{3}\Rightarrow \frac{DF}{CD}=\frac{3}{4}\Rightarrow \frac{DF}{BC}=\frac{3}{4}\Rightarrow DF=\frac{3}{4}BC$ (2)

Từ (1) và (2) suy ra  $BG.DH=BC.\frac{3}{4}BC=\frac{3}{4}B{C}^2$ (đpcm).