Cho hình thang vuông ABCD với đường cao AB  = 2a, các cạnh đáy AD = a và BC = 3a. Gọi M là điểm trên đoạn AC sao cho  $\overrightarrow{AM}=k\overrightarrow{AC}$. Tìm k để BM ⊥ CD

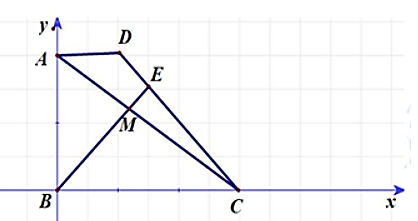
Chọn hệ trục tọa độ như hình vẽ sao cho gốc tọa độ trùng với điểm B, điểm A thuộc Oy và điểm C thuộc Ox.

Theo bài ra ta có:

B(0;0), C(3;0), A(0;2), D(1;2)

Khi đó: $\overrightarrow{AC}=\left(3;-2\right)$

Phương trình tham số của AC là: $\left\{\begin{array}{l}x=3t\\ y=2-2t\end{array}\right.$

Gọi M thuộc AC suy ra: M(3t ; 2 – 2t)

Ta có: $\overrightarrow{BM}=\left(3t;2-2t\right);\overrightarrow{DC}=\left(2;-2\right)$

Để BM ⊥ CD thì $\overrightarrow{BM}.\overrightarrow{DC}=0$

⇔ 6t – 4 + 4t = 0

⇔ t = $\frac{2}{5}$

⇒ $M\left(\frac{6}{5};\frac{6}{5}\right)$

Khi đó: $\overrightarrow{AM}=\left(\frac{6}{5};\frac{-4}{5}\right)$  ⇒ $AM=\frac{\sqrt{52}}{5}$

$\overrightarrow{AC}=\left(3;-2\right)$⇒ $AC=\sqrt{13}$

Vì $\overrightarrow{AM}=k\overrightarrow{AC}$  và $\overrightarrow{AM},\overrightarrow{AC}$   cùng chiều nên k = $\frac{AM}{AC}=\frac{\sqrt{52}}{5\sqrt{13}}=\frac{2}{5}$ .