Cho hình thang vuông ABCD góc A = góc D =90 độ có góc BMC = 90 độ
Cho hình thang vuông ABCD (\(\widehat A\) = \(\widehat D\)= 90°) có \[\widehat {BMC}\]= 90°, với M là trung điểm của AD. Chứng minh: AD là tiếp tuyến của đường tròn bán kính BC.
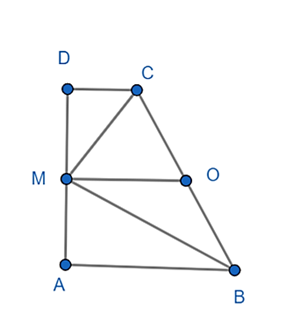
Gọi O là trung điểm BC.
OM là đường trung bình trong hình thang ABCD.
Do đó, OM // AB // DC hay OM ⊥ AD. (1)
Tam giác BMC vuông tại M nên O là tâm đường tròn ngoại tiếp tam giác MBC. (2)
Từ (1) và (2) suy ra AD là tiếp tuyến tại M của đường tròn tâm O.
Vậy AD là tiếp tuyến của đường tròn đường kính BC.