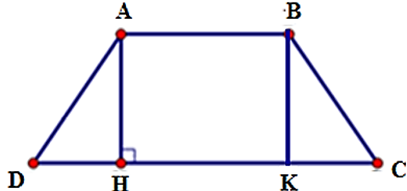
Kẻ AH, BK vuông góc DC

AB // DC nên AH, BK vuông góc AB.

Có: ABHK là hình chữ nhật vì \(\widehat {AHK} = \widehat {BKH} = \widehat {HAB} = 90^\circ \)

Suy ra: AH = BK và AB = HK = 5cm

Xét tam giác ADH và tam giác BKC có:

AD = BC

\(\widehat {AHD} = \widehat {BKC} = 90^\circ \)

AH = BK

⇒ ∆AHD = ∆BKC (c.g.c)

⇒ DH = KC

Mà DH + KC + HK = DC

Suy ra: DH = HK = (DC – HK) : 2 = (DC – AB) : 2 = (11 – 5) : 2 = 3(cm)

HC = DC – DH = 11 – 3 = 8(cm)

Áp dụng hệ thúc lượng trong tam giác ADC vuông ta có:

AH² = DH.HC = 8.3 = 24

AH = \(\sqrt {24} \left( {cm} \right)\)

Áp dụng định lý Pytago trong tam giác ADH vuông tại H:

AD² = AH² + DH²

AD = \(\sqrt {24 + {3^2}} = \sqrt {33} \)

Chu vi hình thang là: AB + BC + CD + AD = 5 + \(2\sqrt {33} \) + 11 = 16 + \(2\sqrt {33} \)

S_ABCD = \(\frac{{\left( {AB + CD} \right).AH}}{2} = \frac{{16\sqrt {24} }}{2} = 8\sqrt {24} = 16\sqrt 6 \left( {c{m^2}} \right)\).