Cho hình nón đỉnh S, đường cao SO, A và B là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ O đến mặt phẳng (SAB) bằng a căn bậc hai của 3 /3 và góc SAO = 30^0, góc AB = 60^0. Độ dài đư
27
24/07/2024
Cho hình nón đỉnh S, đường cao SO, A và B là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ O đến mặt phẳng (SAB) bằng \(\frac{{a\sqrt 3 }}{3}\) và \(\widehat {SAO} = 30^\circ ,\,\,\widehat {SAB} = 60^\circ \). Độ dài đường sinh của hình nón theo a bằng
A. \(a\sqrt 2 \).
B. \(a\sqrt 3 \).
C. \(2a\sqrt 3 \).
D. \(a\sqrt 5 \).
Trả lời
Lời giải
Đáp án đúng là: A
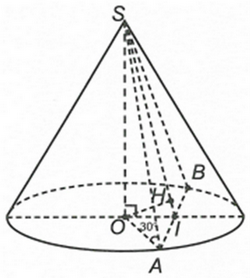
Gọi I là trung điểm của AB. Dựng OH ⊥ SI.
Ta có \(OH = \frac{{a\sqrt 3 }}{3}\).
Vì \(\widehat {SAB} = 60^\circ \) và SA = SB nên tam giác SAB đều.
Suy ra SA = SB = AB.
Tam giác SAO vuông tại O:
\(SO = SA.\sin \widehat {SAO} = \frac{1}{2}SA\) và \[OA = SA.\cos \widehat {SAO} = \frac{{\sqrt 3 }}{2}SA\].
Tam giác SOI vuông tại O có OH là đường cao:
\(\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{I^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{A^2} - A{I^2}}}\).
\( = \frac{4}{{S{A^2}}} + \frac{1}{{\frac{3}{4}S{A^2} - \frac{1}{4}S{A^2}}} = = \frac{4}{{S{A^2}}} + \frac{2}{{S{A^2}}} = \frac{6}{{S{A^2}}}\).
Suy ra \(S{A^2} = 6O{H^2} = 6.\frac{{{a^2}}}{3} = 2{a^2}\).
Do đó \(SA = a\sqrt 2 \).
Vậy ta chọn phương án A.
