Cho hình nón đỉnh S có đáy là hình tròn tâm O. Một mặt phẳng đi qua đỉnh hình
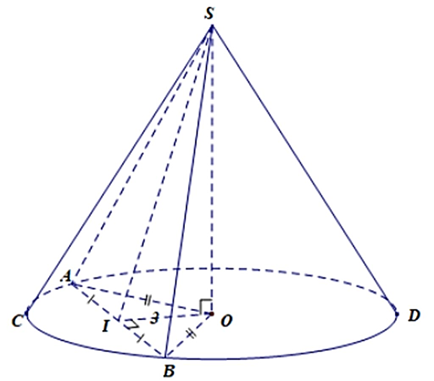
Cho hình nón đỉnh S có đáy là hình tròn tâm O. Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo một thiết diện là tam giác vuông SAB có diện tích bằng 4a2. Góc giữa trục SO và mặt phẳng (SAB) bằng 30°. Tính diện tích xung quanh của hình nón đã cho.