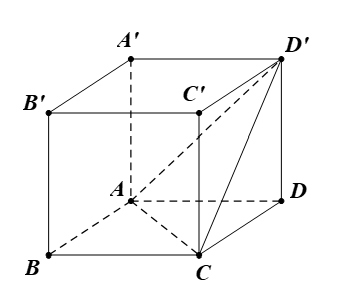
Cho hình lập phương ABCD.A’B’C’D’ có diện tích tam giác ACD’ bằng $a^2\sqrt{3}$ . Tính thể tích V của hình lập phương.

Gọi x là độ dài cạnh của hình lập phương ABCD.A’B’C’D’ (x > 0).

Ta có $C{D}^{\text{'}}=A{D}^{\text{'}}=AC=\sqrt{A{B}^2+B{C}^2}=\sqrt{x^2+x^2}=x\sqrt{2}$ .

Suy ra ∆ACD’ đều.

Do đó $\widehat{CA{D}^{\text{'}}}=60°$ .

Theo đề, ta có $S_{\Delta AC{D}^{\text{'}}}=a^2\sqrt{3}$ .

$\iff \frac{1}{2}A{D}^{\text{'}}.AC.\sin \widehat{CA{D}^{\text{'}}}=a^2\sqrt{3}$.

$\iff x\sqrt{2}.x\sqrt{2}.\sin 60°=2a^2\sqrt{3}$.

⇔ x² = 2a².

$\iff x=a\sqrt{2}$.

Vậy thể tích của hình lập phương ABCD.A’B’C’D’ là: $V=x^3={\left(a\sqrt{2}\right)}^3=2\sqrt{2}{a}^3$ .

Do đó ta chọn phương án C.