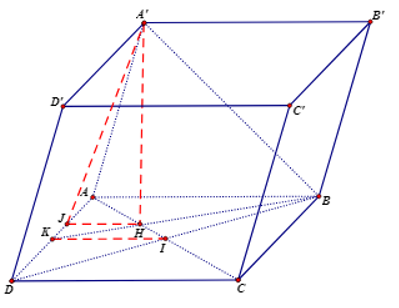
Cho hình lăng trụ tứ giác ABCD.A’B’C’D’ có đáy ABCD là hình vuông tâm là I và có diện tích bằng 9a^2.
24
20/08/2024
Cho hình lăng trụ tứ giác ABCD.A’B’C’D’ có đáy ABCD là hình vuông tâm là I và có diện tích bằng 9a2. Hình chiếu của đỉnh A’ trên mặt đáy (ABCD) là điểm H thỏa mãn . Biết rằng . Tính góc giữa mặt phẳng (ADA’) và mặt phẳng (ABCD)
A. 45°;
B. 60°;
C. 90°;
D. 30°.
Trả lời
Đáp án đúng là: A
Xét tam giác ABD có và AI là trung tuyến nên H là trọng tâm tam giác
Kéo dài BH cắt AD tại K
Suy ra K là trung điểm của AD và
Vì SABCD = 9a2 nên AB = BC = CD = DA = 3a
Xét tam giác ABK vuông ở A có BK2 = AB2 + AK2
Suy ra
Trong mp(ABCD) dựng HJ // AB (J ∈ AD)
Suy ra AD ⊥ HJ (1)
Mà AD ⊥ HA’, do đó AD ⊥ (A’HJ)
Suy ra AD ⊥ A’J (2)
Ta có (A’AD) ∩ (ABCD) = AD (3)
Từ (1), (2) và (3) suy ra
Xét tam giác A’HB vuông tại H có A’B2 = HB2 + A’H2
Suy ra
Xét tam giác AKI có KI // JH
Suy ra
Do đó
Xét tam giác A’HB vuông tại H có JH = A’H = a
Suy ra tam giác A’HJ vuông cân tại H
Do đó
Vậy ta chọn đáp án A.