Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của AB (Hình 100).
8
10/11/2024
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của AB (Hình 100).
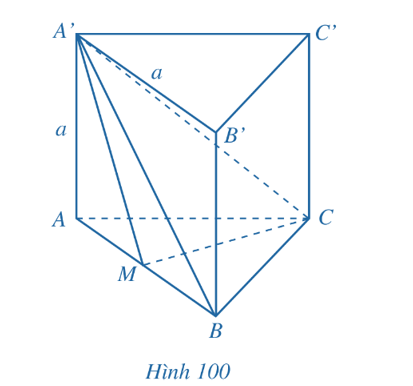
a) Tính góc giữa hai đường thẳng AB và B’C’.
Trả lời
Vì ABC.A’B’C’ là hình lăng trụ tam giác đều có tất cả các cạnh bằng a nên ta có:
⦁ Các mặt bên A’C’CA, B’C’CB, A’B’BA đều là hình vuông cạnh a.
⦁ Hai mặt đáy ABC và A’B’C’ là hai tam giác đều cạnh a và hai mặt phẳng chứa hai mặt đáy song song với nhau.
⦁ Các cạnh bên AA’, BB’, CC’ đều vuông góc với mặt phẳng đáy (ABC) và (A’B’C’).
a) Do B’C’CB là hình vuông nên BC // B’C’.
Suy ra góc giữa hai đường thẳng AB và B’C’ bằng góc giữa hai đường thẳng AB và BC và bằng
Mặt khác ABC là tam giác đều nên
Vậy góc giữa hai đường thẳng AB và B’C’ bằng 60°.

