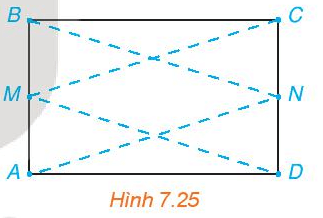
Cho hình chữ nhật ABCD và M, N tương ứng là trung điểm của các cạnh AB, CD (H.7.25). Chứng minh rằng bốn điểm

Luyện tập 3 trang 51 Toán 10 Tập 2: Cho hình chữ nhật ABCD và M, N tương ứng là trung điểm của các cạnh AB, CD (H.7.25). Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một hypebol có hai tiêu điểm là M và N.

Trả lời

Do ABCD là hình chữ nhật nên AB = CD. 

Vì M, N tương ứng là trung điểm của các cạnh AB, CD nên AM = BM = $\frac{1}{2}$AB và CN = DN = $\frac{1}{2}$CD. 

Do đó ta có: BM = CN = AM = DN  (*). 

Khi đó BM // = ND nên BMDN là hình bình hành, suy ra BN = MD (1). 

Tương tự AN = CM (2). 

Hơn nữa ta chứng minh được BMNC là hình chữ nhật nên hai đường chéo BN và MC bằng nhau hay BN = MC (3). 

Từ (1), (2) và (3) suy ra: BN = CM = AN = DM (**).

Từ (*) và (**) ta có: |BN – BM| = |CN – CM| = |AN – AM| = |DN – DM| < MN (bất đẳng thức tam giác).

Vậy A, B, C, D cùng thuộc một hypebol có hai tiêu điểm là M và N.