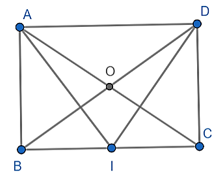
Cho hình chữ nhật ABCD, tâm O, AB = 4, BC = 3. I là trung điểm BC. Tính
Cho hình chữ nhật ABCD, tâm O, AB = 4, BC = 3. I là trung điểm BC. Tính \(\left| {\overrightarrow {IA} - \overrightarrow {DI} } \right|;\left| {\overrightarrow {IA} + \overrightarrow {IB} } \right|\).