Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm của AB, BC

Bài 1 trang 23 Chuyên đề Toán lớp 11: Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm của AB, BC. Xác định phép tịnh tiến biến tam giác AMO thành tam giác ONC.

Trả lời

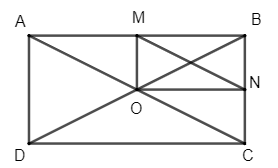
Vì O là giao điểm hai đường chéo của hình chữ nhật ABCD nên O là trung điểm của AC.

Suy ra $\overrightarrow{AO}=\overrightarrow{OC}=\frac{1}{2}\overrightarrow{AC}$ (1).

Ta có M, N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC, suy ra MN // AC và MN = $\frac{1}{2}AC$. Do đó, $\overrightarrow{MN}=\frac{1}{2}\overrightarrow{AC}$(2).

Từ (1) và (2) suy ra $\overrightarrow{AO}=\overrightarrow{OC}=\overrightarrow{MN}$.

Khi đó, ta có phép tịnh tiến theo vectơ $\overrightarrow{AO}$ biến các điểm A, M, O lần lượt thành các điểm O, N, C.

Vậy phép tịnh tiến theo vectơ $\overrightarrow{AO}$ biến tam giác AMO thành tam giác ONC.

Xem thêm các bài giải Chuyên đề Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 1: Phép dời hình

Bài 2: Phép đồng dạng

Bài 1: Một vài yếu tố của lí thuyết đồ thị. Đường đi Euler và đường đi Hamilton

Bài 2: Một vài ứng dụng của lí thuyết đồ thị

Bài 1: Một số nội dung cơ bản về vẽ kĩ thuật

Bài 2: Đọc và vẽ bản vẽ kĩ thuật đơn giản