Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.
a) Tứ giác ADFE là hình gì? Vì sao?
b) Tứ giác EMFN là hình gì? Vì sao?
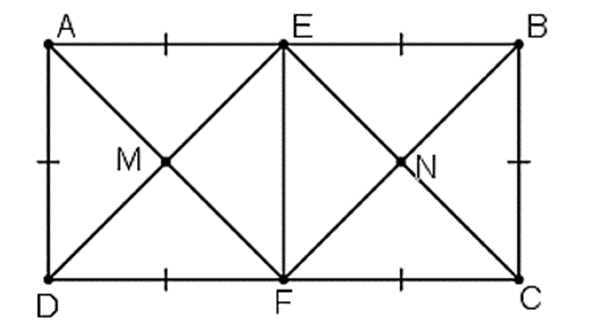
a) E, F là trung điểm AB, CD ⇒ AE = EB = \(\frac{{AB}}{2}\), DF = FC = \(\frac{{CD}}{2}\).
Ta có: AB = CD = 2AD = 2BC
⇒ AE = EB = BC = CF = FD = DA.
+ Tứ giác ADFE có AE // DF, AE = DF
⇒ ADFE là hình bình hành.
Hình bình hành ADFE có \(\widehat A\) = 90º
⇒ ADFE là hình chữ nhật.
Hình chữ nhật ADFE là hình chữ nhật có AE= AD
⇒ ADFE là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành
Do đó DE // BF
Tương tự: AF // EC
Suy ra EMFN là hình bình hành
Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.
Hình bình hành EMFN có \(\widehat M\)= 90º nên là hình chữ nhật.
Lại có ME = MF nên EMFN là hình vuông.