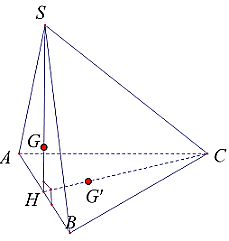
Xét ∆SAB là tam giác đều:

Gọi H là trung điểm AB suy ra SH ^ (ABC) và  $SH=\frac{\sqrt{3}}{2}.1=\frac{\sqrt{3}}{2}$.

Gọi G là trọng tâm ∆SAB suy ra:

$GS=GA=GB=\frac{2}{3}SH=\frac{2}{3}.\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$ 

 G' là trọng tâm ∆ABC suy ra:

$G\text{'}A=G\text{'}B=G\text{'}C=\frac{2}{3}CH=\frac{2}{3}.\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$

Suy ra bán kính khối cầu ngoại tiếp hình chóp S.ABC là:

$R=\sqrt{G{S}^2+G\text{'}{B}^2-\frac{A{B}^2}{4}}=\sqrt{{\left(\frac{\sqrt{3}}{3}\right)}^2+{\left(\frac{\sqrt{3}}{3}\right)}^2-\frac{1^2}{4}}=\frac{\sqrt{15}}{6}$

Vậy thể tích khối cầu ngoại tiếp hình chóp S.ABC là:

 $V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi .{\left(\frac{\sqrt{15}}{6}\right)}^3=\frac{5\pi \sqrt{15}}{54}$.