Cho hình chóp tứ giác đều S.ABCD có  $SA=\sqrt{11}a$, côsin của góc hợp bởi hai mặt phẳng (SBC); và (SCD) bằng  $\frac{1}{10}$. Tính thể tích của khối chóp S.ABCD.

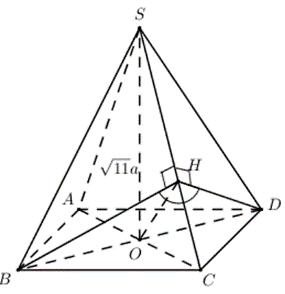
Gọi x là độ dài cạnh đáy của chóp đều S.ABCD.

Gọi O = AC Ç BD Þ SO ^ (ABCD)

Ta có:  $\left\{\begin{array}{l}BD\perp AC\left(gt\right)\\ BD\perp SO\left(doSO\perp \left(ABCD\right)\right)\end{array}\right.$

$\Rightarrow BD\perp \left(SAC\right)\Rightarrow BD\perp SC$

Trong (SBC) kẻ BH ^ SC (H Î SC) có:

•  $\left\{\begin{array}{l}BH\perp SC\\ BD\perp SC\left(cmt\right)\end{array}\right.\Rightarrow SC\perp \left(BDH\right)\Rightarrow SC\perp DH$

•  $\left\{\begin{array}{l}\left(SBC\right)\cap \left(SCD\right)=SC\\ \left(SBC\right)\supset BH\perp SC\\ \left(SBC\right)\supset DH\perp SC\end{array}\right.\Rightarrow \left(\widehat{\left(SBC\right);\left(SCD\right)}\right)=\left(\widehat{BH;DH}\right)$

$\Rightarrow \left[\begin{array}{l}\cos \widehat{BHD}=\frac{1}{10}\\ \cos \widehat{BHD}=-\frac{1}{10}\end{array}\right.$

Ta dễ dàng chứng minh được: ∆BHC = ∆DHC

Þ HB = HD Þ ∆HBD cân tại H

Xét tam giác SBC ta có: 

$\cos \widehat{C}=\frac{B{C}^2+S{C}^2-S{B}^2}{2.BC.SC}=\frac{x^2}{2x.\sqrt{11}a}=\frac{x\sqrt{11}}{22a}$

$\Rightarrow HC=BC.\cos \widehat{C}=\frac{x^2\sqrt{11}}{22a}$

$\Rightarrow HB=\sqrt{B{C}^2-H{C}^2}=\sqrt{x^2-\frac{x^4}{44a^2}}=\frac{x\sqrt{a^2-x^2}}{2a\sqrt{11}}=HD$

Xét tam giác BDH có: 

$\cos \widehat{BHD}=\frac{H{B}^2+H{D}^2-B{D}^2}{2HB.HD}=\frac{2x^2-\frac{x^4}{22a^2}-2x^2}{2\left(x^2-\frac{x^4}{44a^2}\right)}$

$=\frac{2x^2-\frac{x^4}{22a^2}-2x^2}{2x^2-\frac{x^4}{22a^2}}=1-\frac{44x^2{a}^2}{44x^2{a}^2-x^4}$

+) TH1:  $\cos \widehat{BHD}=\frac{1}{10}$ 

$\iff 1-\frac{44x^2{a}^2}{44x^2{a}^2-x^4}=\frac{1}{10}$

$\iff \frac{44x^2{a}^2}{44x^2{a}^2-x^4}=\frac{9}{10}$

Û 440x²a² = 396x²a² − 9x⁴

Û 9x⁴ = −44x²a² (vô nghiệm)

+) TH2:  $\cos \widehat{BHD}=-\frac{1}{10}$ 

$\iff 1-\frac{44x^2{a}^2}{44x^2{a}^2-x^4}=-\frac{1}{10}$

$\iff \frac{44x^2{a}^2}{44x^2{a}^2-x^4}=\frac{11}{10}$

Û 440x²a² = 484x²a² − 11x⁴

Û 11x⁴ = 44x²a²

Û x² = 4a²

Û x = 2a 

$\Rightarrow OA=\frac{1}{2}AC=\frac{1}{2}.2a\sqrt{2}=a\sqrt{2}$

Xét tam giác vuông SOA có:

 $SO=\sqrt{S{A}^2-O{A}^2}=\sqrt{11a^2-2a^2}=3a$.

Vậy  $V_{S.ABCD}=\frac{1}{3}SO.S_{ABCD}=\frac{1}{3}.3a.{\left(2a\right)}^2=4a^3$.