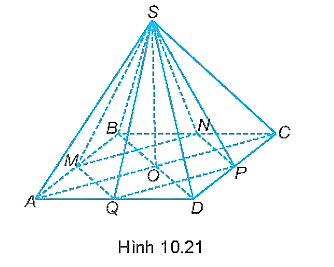
Cho hình chóp tứ giác đều S.ABCD có thể tích bằng 144 cm^3. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA (H.10.21). Tính thể tích của hình chóp S.MNPQ.
34
29/10/2024
Cho hình chóp tứ giác đều S.ABCD có thể tích bằng 144 cm3. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA (H.10.21). Tính thể tích của hình chóp S.MNPQ.
Trả lời
Lời giải
Gọi O là giao điểm của AC và BD.
Vì M, N lần lượt là trung điểm của AB, BC nên MN là đường trung bình của tam giác ABC, do đó MN=12AC.
Tương tự, MQ là đường trung bình của tam giác ABD nên MQ=12BD.
Vì ABCD là hình vuông nên ta cũng chứng minh được MNPQ là hình vuông và hình chóp S.MNPQ là hình chóp tứ giác đều.
Diện tích hình vuông MNPQ là:
SMNPQ=MN⋅MQ=12AC⋅12BD=12(12AC⋅BD)=12SABCD.
(Vì ABCD là hình vuông nên nó cũng là hình thoi, do đó diện tích của nó có thể tính bằng tích hai đường chéo).
Hai hình chóp S.ABCD và S.MNPQ có chung chiều cao SO và SMNPQ=12SABCD nên
VS.MNPQ=12VS.ABCD=12⋅144=72 (cm3).