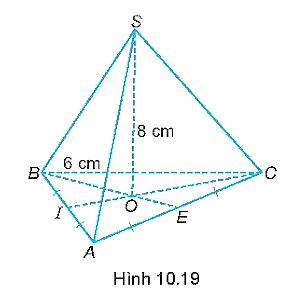
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 6 cm, chiều cao 8 cm như Hình 10.19. Tính thể tích hình chóp

Trả lời

Lời giải

Ta có IC, BE là các đường cao của tam giác đều ABC.

O là giao điểm của BE và IC, khi đó SO là đường cao của hình chóp tam giác đều S.ABC.

Tam giác ABC là tam giác đều nên AB = BC = 6 cm.

CI là đường cao đồng thời là đường trung tuyến. Do đó, ta có: \(BI = \frac{1}{2}AB = 3\) (cm).

Áp dụng định lí Pythagore vào tam giác CBI vuông tại I có:

BI² + IC² = BC²

Suy ra IC² = BC² – BI² = 6² – 3² = 27.

Do đó, BI = \(\sqrt {27} \approx 5,2\) (cm).

Diện tích tam giác ABC là:

\(S = \frac{1}{2}IC \cdot AB \approx \frac{1}{2} \cdot 5,2 \cdot 6 = 15,6\) (cm²).

Thể tích hình chóp là: \(V = \frac{1}{3}S \cdot SO \approx \frac{1}{3} \cdot 15,6 \cdot 8 = 41,6\) (cm³).