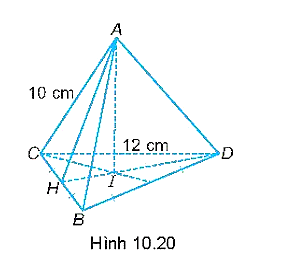
Cho hình chóp tam giác đều A.BCD có cạnh đáy bằng 12 cm, cạnh bên bằng 10 cm như (H.10.20). Tính diện tích xung quanh của hình chóp.

Lời giải

Ta có DH là đường cao của tam giác BCD.

Vì tam giác BCD đều nên BC = DB = CD = 12 cm và DH là đường cao đồng thời là đường trung tuyến của tam giác. Do đó, \(HC = \frac{1}{2}CB = 6\) cm.

Tam giác ABC cân tại A nên AH là đường trung tuyến đồng thời là đường cao, vậy AH là một trung đoạn của hình chóp A.BCD.

Áp dụng định lí Pythagore vào tam giác CHA vuông tại H có:

HA² + HC² = CA²

Suy ra HA² = CA² – CH² = 10² – 6² = 64 nên HA = 8 cm.

Chu vi tam giác DBC là: BD + BC + CD = 12 + 12 + 12 = 36 (cm).

Diện tích xung quanh hình chóp là:

\({S_{xq}} = p \cdot d = \frac{1}{2} \cdot 36 \cdot 8 = 144\) (cm²).