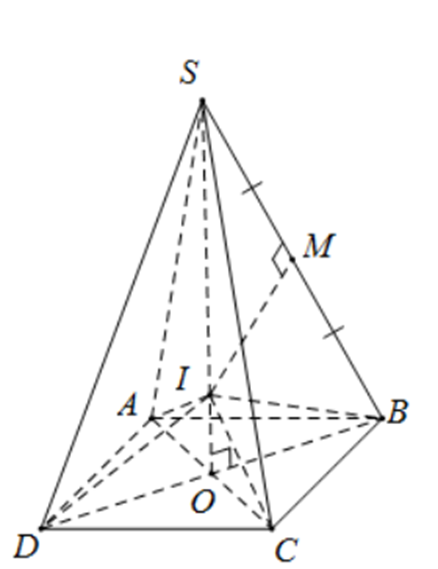
Vì S.ABCD là hình chóp đều nên đường cao SO của hình chóp cũng chính là trục của đa giác đáy 

Xét ΔBCD vuông cân tại C có  BC = CD = a

⇒ BD = \(\sqrt {B{C^2} + C{D^2}} = a\sqrt 2 \)

⇒ BO = \(\frac{1}{2}BD = \frac{{a\sqrt 2 }}{2}\)

Xét ΔSOB vuông tại O có  SB = 2a ,  BO = \(\frac{{a\sqrt 2 }}{2}\)

⇒ SO = \(\sqrt {S{B^2} - B{O^2}} = \frac{{a\sqrt {14} }}{2}\)

Trong mặt phẳng (SOB), ta vẽ trung trực của SB, đường này cắt SO tại I. Rõ ràng I là tâm mặt cầu ngoại tiếp S.ABCD

Gọi M là trung điểm của SB

⇒ SM = \(\frac{1}{2}SB = a\)

 Xét ΔSMI và ΔSOB ta có:

Chung \(\widehat S\)

\(\widehat {SMI} = \widehat {SOB} = 90^\circ \)

⇒ ΔSMI ~ΔSOB (g.g)

⇒ \(\frac{{SI}}{{SB}} = \frac{{SM}}{{SO}}\)

⇒ SI = \(\frac{{SB.SM}}{{SO}} = \frac{{2a.a}}{{\frac{{a\sqrt {14} }}{2}}} = \frac{{2a\sqrt {14} }}{7}\)

Vì SI chính là bán kính mặt cầu ngoại tiếp S.ABCD nên ta có:

V_{khối cầu} = \(\frac{4}{3}\)π.SI³ = \(\frac{{64\pi \sqrt {14} }}{{147}}\).