Cho hình chóp tam giác S.ABC. Gọi M là trung điểm của SB, N thuộc cạnh SC sao cho NS
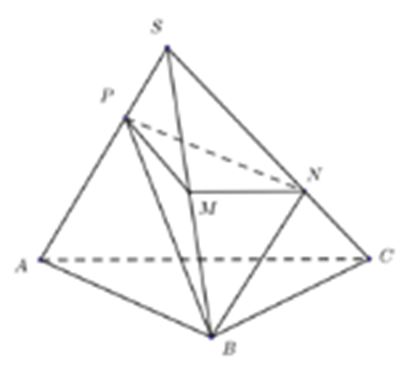
Cho hình chóp tam giác S.ABC. Gọi M là trung điểm của SB, N thuộc cạnh SC sao cho NS = 2NC, P thuộc cạnh SA sao cho PA = 2PS. Gọi V1, V2 lần lượt là thể tích của các khối tứ diện BMNP và SABC. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}.\)