Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng 9 cm, SH là chiều cao. Gọi M là trung điểm của BC

Bài 5 trang 74 SBT Toán 8 Tập 1: Cho hình chóp tam giác đều $S.ABC$ có độ dài cạnh đáy bằng 9 cm, $SH$ là chiều cao. Gọi $M$ là trung điểm của $BC$ (Hình 5). Tính thể tích của hình chóp $S.ABC$, biết $H$ là trọng tâm của tam giác $ABC$, $AH=\frac{\sqrt{3}}{3}AB$ và $SH=2AH$.

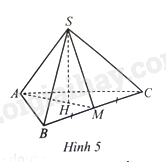
Trả lời

Ta có: $AH=\frac{\sqrt{3}}{3}AB$ nên $AH=3\sqrt{3}$ cm. Suy ra $SH=2AH=6\sqrt{3}$ cm.

Do $H$ là trọng tâm của tam giác $ABC$ nên $AH=\frac{2}{3}AM$.

Suy ra $AM=\frac{3}{2}AH=\frac{9\sqrt{3}}{2}$ cm.

$\mathrm{\Delta }ABM=\mathrm{\Delta }ACM$(c-c-c) suy ra $\widehat{AMB}=\widehat{AMC}={90}^{\circ }$. Do đó $AM\mathrm{\perp }BC$.

Diện tích của hình chóp tam giác đều đó là:

$S_{ABC}=\frac{1}{2}.BC.AM=\frac{81\sqrt{3}}{4}\left(c{m}^2\right)$

Thể tích của hình chóp tam giác đều đó là: $\frac{1}{3}.S_{ABC}.SH=\frac{243}{2}\left(c{m}^2\right)$.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)

Bài tập cuối chương 3

Bài 1: Hình chóp tam giác đều

Bài 2: Hình chóp tứ giác đều

Bài tập cuối chương 4 trang 78

Bài 1: Định lí Pythagore