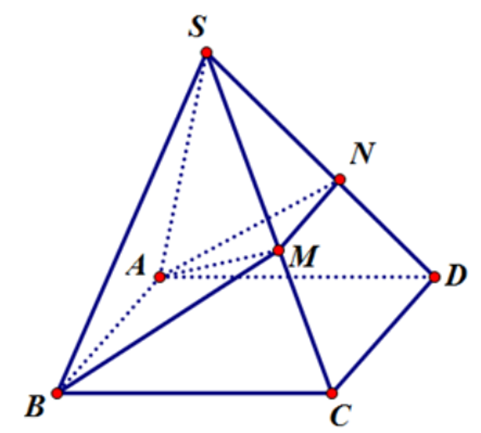
Ta có (α) ∩ (SCD) = NM ⇒ NM // CD.

Do đó (α) là (ABMN).

Mặt phẳng (α) chia khối chóp thành 2 phần có thể tích bằng nhau là:

\({V_{S.ABMN}} = {v_{ABCDNM}}\)

⇒ \({V_{S.ABMN}} = \frac{1}{2}{V_{S.ABCD}}\) (1)

Ta có: \({V_{S.ABC}} = {V_{S.ACD}} = \frac{1}{2}{V_{S.ABCD}}\)

Đặt \(\frac{{SN}}{{SD}} = x\) với (0 < x < 1).

Khi đó theo định lí Ta – let ta có: \(\frac{{SN}}{{SD}} = \frac{{SM}}{{SC}} = x\)

Mặt khác \(\frac{{{V_{S.ABM}}}}{{{V_{S.ABC}}}} = \frac{{SA}}{{SA}}.\frac{{SB}}{{SB}}.\frac{{SM}}{{SC}} = x\)

⇒ \({V_{S.ABM}} = \frac{x}{2}.{V_{S.ABCD}}\)

\(\frac{{{V_{S.AMN}}}}{{{V_{S.ACD}}}} = \frac{{SA}}{{SA}}.\frac{{SM}}{{SC}}.\frac{{SN}}{{SD}} = {x^2}\) ⇒ \({V_{S.AMN}} = \frac{{{x^2}}}{2}.{V_{S.ABCD}}\)

⇒ \({V_{S.ABMN}} = {V_{S.ABM}} + {V_{S.AMN}} = \left( {\frac{x}{2} + \frac{{{x^2}}}{2}} \right).{V_{S.ABCD}}\) (2)

Từ (1) và (2) suy ra \(\frac{x}{2} + \frac{{{x^2}}}{2} = \frac{1}{2}\) ⇔ x² + x – 1 = 0

⇔ \(\left[ {\begin{array}{*{20}{c}}{x = \frac{{ - 1 - \sqrt 5 }}{2}}\\{x = \frac{{ - 1 + \sqrt 5 }}{2}}\end{array}} \right.\)

Đối chiếu điều kiện của x ta được \(\frac{{SN}}{{SD}} = \frac{{ - 1 + \sqrt 5 }}{2}.\)