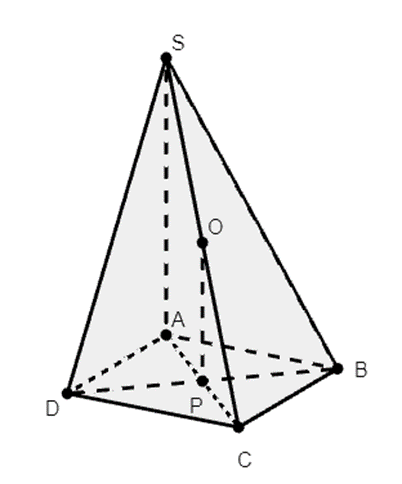
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên \(SA = a\sqrt 6 \) vuông góc với đáy (ABCD). Tính theo a diện tích mặt cầu ngoại tiếp hình chóp S.ABCD.

A. 8πa²;

B. 2 πa²;

C. 2a²;

D. \({a^2}\sqrt 2 \).

Đáp án đúng là: A

Tâm của mặt cầu là trung điểm O của đoạn thẳng SC.

Ta có: R = OA = OB = OC = OD = SO

= \(\frac{1}{2}SC = \frac{1}{2}\sqrt {S{A^2} + A{C^2}} \)

\( = \frac{1}{2}\sqrt {S{A^2} + A{B^2} + B{C^2}} = a\sqrt 2 \)

⇒ S = 4 πR² = 8 πa².