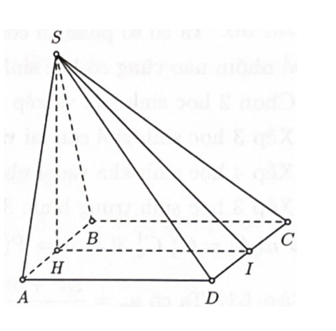
Cho hình chóp SABCD có đáy là hình chữ nhật, AB = 2a, AD = a; tam giác SAB đều và nằm trong mặt phẳng vuông góc

Cho hình chóp SABCD có đáy là hình chữ nhật, AB = 2a, AD = a; tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Góc $\alpha$ tạo bởi hai mặt phẳng (SCD) và (ABCD) có số đo bằng

Trả lời

+) Gọi H là trung điểm AB, do tam giác SAB đều nên $SH\perp AB.$ Mà $\left(SAB\right)\perp \left(ABCD\right)$ nên $SH\perp \left(ABCD\right).$

+) Gọi I là trung điểm CD.

Ta có: $\alpha =\left(\right(SCD);(ABCD\left)\right)=\widehat{SIH}.$

+) Trong đó: SH là đường cao của tam giác đều cạnh 2a nên $SH=a\sqrt{3},HI=AD=a.$

+) Khi đó $\tan \alpha =\tan \widehat{SIH}=\frac{SH}{HI}=\sqrt{3},$suy ra $\alpha =60°.$