Luyện tập 4 trang 36 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là một hình vuông, SA ⊥ (ABCD). Kẻ AH vuông góc với SC (H thuộc SC), BM vuông góc với SC (M thuộc SC). Chứng minh rằng SC ⊥ (MBD) và AH // (MBD).
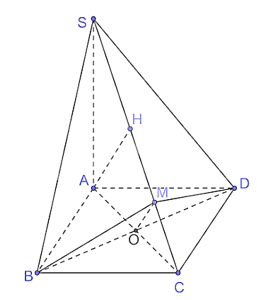
Vì ABCD là hình vuông nên AC ⊥ BD.
Vì SA ⊥ (ABCD) nên SA ⊥ BD mà AC ⊥ BD nên BD ⊥ (SAC).
Do BD ⊥ (SAC) nên BD ⊥ SC.
Vì BM ⊥ SC mà BD ⊥ SC nên SC ⊥ (BMD).
Gọi O là giao điểm của AC và BD.
Vì SC ⊥ (BMD) nên SC ⊥ OM.
Lại có AH ⊥ SC và SC ⊥ OM nên AH // OM.
Vì AH // OM và OM (MBD) nên AH // (MBD)
Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác: