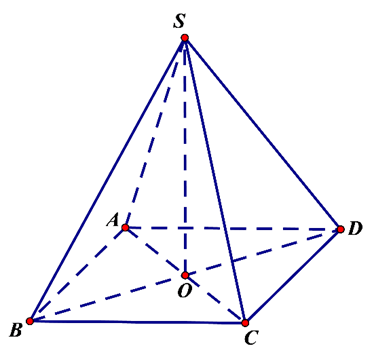
Cho hình chóp S.ABCD, có đáy ABCD là hình vuông. SA = SC; SB = SD; O
Cho hình chóp S.ABCD, có đáy ABCD là hình vuông. SA = SC; SB = SD; O = AC giao BD.
a) Chứng minh: SO vuông góc với mặt phẳng (ABCD).
b) Chứng minh: BD vuông góc với (SAC) và AC vuông góc với mặt phẳng (SBD).
c) Chứng minh: (SBD) vuông góc với (SAC); (SBD) vuông góc với (ABCD).