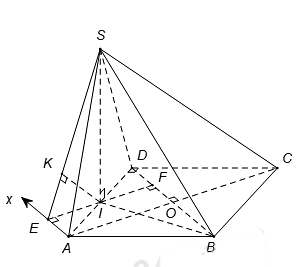
Gọi I là trung điểm của AD nên suy ra SI ^ AD Þ SI ^ (ABCD) và  $SI=\frac{a\sqrt{3}}{2}$.

Kẻ Ax // BD.

Do đó d(BD; SA) = d(BD; (SAx)) = d(D; (SAx)) = 2d(I; (SAx))

Kẻ IE ^ Ax, kẻ IK ^ SE (1) ta có:

$\left\{\begin{array}{l}Ax\perp SI\\ Ax\perp IE\end{array}\right.\Rightarrow Ax\perp \left(SIE\right)\Rightarrow Ax\perp IK\left(2\right)$

Từ (1) và (2) suy ra IK ^ (SAx)

Khi đó d(I; (SAx)) = IK

Gọi F là hình chiếu của I trên BD, ta dễ dàng chứng minh được:

ΔIAE = ΔIDF (cạnh huyền – góc nhọn)

Thật vậy, xét ΔIAE vuông tại E và ΔIDF vuông tại F có:

 $\widehat{IAE}=\widehat{IDF}$ (do Ax // BD, hai góc ở vị trí so le trong)

IA = ID (Do I là trung điểm của AD)

Suy ra ΔIAE = ΔIDF (cạnh huyền – góc nhọn)

$\Rightarrow IE=IF=\frac{AO}{2}=\frac{a\sqrt{2}}{4}$

Tam giác vuông SIE, có 

$IK=\frac{SI.IE}{\sqrt{S{I}^2+I{E}^2}}=\frac{\frac{a\sqrt{3}}{2}.\frac{a\sqrt{2}}{4}}{\sqrt{{\left(\frac{a\sqrt{3}}{2}\right)}^2+{\left(\frac{a\sqrt{2}}{4}\right)}^2}}=\frac{a\sqrt{21}}{14}$

Vậy  $d\left(BD;SA\right)=2IK=2.\frac{a\sqrt{21}}{14}=\frac{a\sqrt{21}}{7}$.