Cho hình chóp S.ABCD có đáy ABCD là hình vuông bằng cạnh bằng a, tam giác SAB là tam giác đều, SC = SD = $a\sqrt{2}$ . Tính thể tích V của khối chóp S.ABCD?

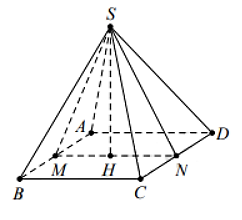
Gọi M, N là trung điểm của AB và CD

MN là đường trung bình của ABCD nên MN // AD // BC

Mà AB ⊥ AD nên MN ⊥ AB

Vì ∆SAB đều nên SM ⊥ AB

Suy ra: AB ⊥ (SMN) ⇒ (SMN) ⊥ (ABCD)

Lại có: ∆SAB đều ⇒ SM = $\frac{a\sqrt{3}}{2}$

Tam giác SCD cân nên: SN ⊥ CD

Áp dụng định lý Pytago trong tam giác SCN ta có:

SN = $\sqrt{S{C}^2-{\left(\frac{CD}{2}\right)}^2}=\sqrt{2a^2-\frac{a^2}{4}}$  = $\frac{a\sqrt{7}}{2}$

Kẻ SH ⊥ MN (H thuộc MN)

Suy ra: SH ⊥ (ABCD)

Mặt khác: S_MNS = $\sqrt{p\left(p-SM\right)\left(p-SN\right)\left(p-MN\right)}$  (công thức Hê–rông)

Mà p = (SM + SN + MN) : 2 = $\left(\frac{a\sqrt{3}}{2}+\frac{a\sqrt{7}}{2}+a\right):2=\frac{a\sqrt{3}+a\sqrt{7}+2a}{4}$

Suy ra: S_MNS = $\sqrt{p\left(p-SM\right)\left(p-SN\right)\left(p-MN\right)}$  = $\frac{a^2\sqrt{3}}{4}$

Mà S_MNS = $\frac{1}{2}.SH.MN$ . Suy ra: SH = $\frac{2S_{MNS}}{MN}=\frac{2.\frac{a^2\sqrt{3}}{4}}{a}=\frac{a\sqrt{3}}{2}$