Cho hình chóp S.ABCD có đáy ABCD là hình thang có đáy lớn BC, đáy nhỏ AD. Mặt bên (SAD) là tam giác đều, (α) là mặt phẳng đi qua M trên cạnh AB, song song với SA, BC. Mp (α) cắt các cạnh CD, SC, SB lần lượt tại N, P, Q. Tứ giác MNPQ là hình gì?
A. Hình thoi
B. Hình bình hành
C. Tứ giác có các cạnh đối cắt nhau
D. Hình thang cân.
Đáp án đúng là: D
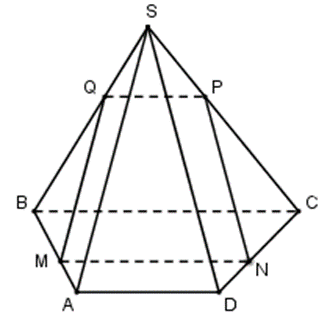
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BC\,{\rm{//}}\,(\alpha ),BC \subset (ABCD),BC \subset (SBC)}\\{(\alpha ) \cap (ABCD) = MN}\\{(\alpha ) \cap (SBC) = PQ}\end{array}} \right. \Rightarrow MN\,{\rm{//}}\,BC\,{\rm{//}}\,PQ\quad \)
Suy ra tứ giác MNPQ là hình thang (1)
Vì \(\left\{ {\begin{array}{*{20}{l}}{(\alpha ) \cap (SAB) = MQ}\\{(\alpha )\,{\rm{//}}\,SA,SA \subset (SAB)}\end{array} \Rightarrow SA\,{\rm{//}}\,MQ} \right.\)
Áp dụng định lý Ta – lét ta có:
\(\begin{array}{l}\frac{{AM}}{{AB}} = \frac{{SQ}}{{SB}} = \frac{{SP}}{{SC}};\frac{{AM}}{{AB}} = \frac{{DN}}{{DC}}\\ \Rightarrow \frac{{SP}}{{SC}} = \frac{{DN}}{{DC}} \Rightarrow NP\,{\rm{//}}\,SD\end{array}\)
Vì \(\left\{ {\begin{array}{*{20}{l}}{MQ\,{\rm{//}}\,SA}\\{MN\,{\rm{//}}\,BC\,{\rm{//}}\,AD}\end{array} \Rightarrow \widehat {NMQ} = \widehat {SAD}} \right.{\rm{ }}\)
Mà tam giác SAD đều nên \(\widehat {SA{\rm{D}}} = 60^\circ \)
Suy ra \(\widehat {NMQ} = 60^\circ \)
Chứng minh tương tự ta có \(\widehat {MNP} = \widehat {SDA} = 60^\circ \)
Do đó \(\widehat {NMQ} = \widehat {MNP}\) (2)
Từ (1) và (2) suy ra MNPQ là hình thang cân
Vậy đáp án cần chọn là: D.