Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD // BC và AD = 2BC. Lấy M trên cạnh SA sao cho MA = 2MS.

a) Chứng minh OM // (SCD).

b) Xác định giao điểm N của MD và mặt phẳng (SBC).

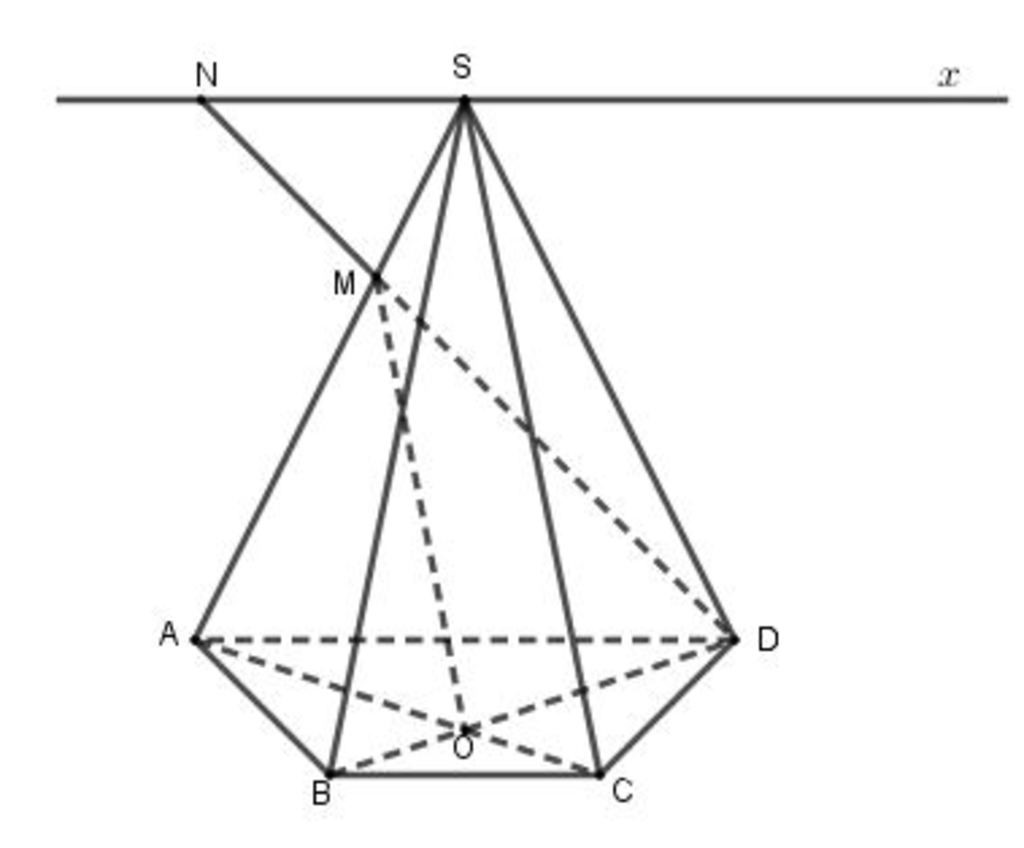
Do AD // BC nên $\frac{AO}{OC}=\frac{AD}{BC}=2$

Mà $\frac{AM}{MS}=2$  nên $\frac{AM}{MS}=\frac{AO}{OC}=2$

⇒OM // SC (định lí Ta–let)

Lại có SC ⊂ (SCD) nên OM//(SCD)

b) Ta có: MD ⊂ (SAD)

* Tìm giao tuyến của (SBC) với (SAD)

Ta có: S ∈ (SAD) ∩ (SBC)

Lại có: $\left\{\begin{array}{l}AD\subset \left(SAD\right)\\ BC\subset \left(SBC\right)\\ AD\parallel BC\end{array}\right.$  ⇒ (SAD) ∩ (SBC) = Sx // AD // BC.

Do đó giao tuyến của (SBC) với (SAD) là đường thẳng đi qua S và song song với AD, BC.

Trong mặt phẳng (SAD), gọi N là giao điểm của MD với Sx.

Khi đó $\left\{\begin{array}{l}N\in MD\\ N\in Sx\subset \left(SBC\right)\end{array}\right.$ ⇒ N = MD ∩ (SBC).