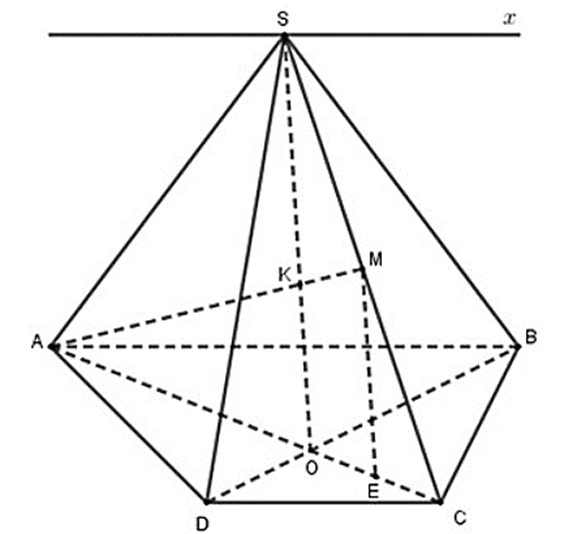
a) S là điểm chung của (SAB) và (SCD)

AB // CD; AB ⊂ (SAB); CD ⊂ (SCD)

Suy ra (SAB) ∩ (SCD) = Sx // AB // CD

b) Ta có: AM ⊂ (SAC)

Dễ thấy S ∈ (SAC) ∩ (SBD)

Gọi O là giao điểm của AC và BD. Khi đó O ∈ AC ⊂ (SAC), O ∈ BD ⊂ (SBD) nên O ∈ (SAC) ∩ (SBD)

Do đó SO = (SAC) ∩ (SBD)

Trong (SAC), gọi K = AM ∩ SO thì K ∈ AM, K ∈ SO ⊂ (SBD) nên K = AM ∩ (SBD)

Do AB // CD nên \(\frac{{OC}}{{OA}} = \frac{{CD}}{{AB}} = \frac{1}{2}\)suy ra \(OA = \frac{2}{3}AC,OC = \frac{1}{3}AC\)

Gọi E là trung điểm của OC suy ra ME là đường trung bình của ∆SCO

Suy ra: ME // SO

Mà \(OE = \frac{1}{2}OC = \frac{1}{2}.\frac{1}{3}AC = \frac{1}{6}AC\)

Suy ra: AE = AO + OE = \(\frac{2}{3}AC + \frac{1}{6}AC = \frac{5}{6}AC\)

⇒ \(\frac{{AK}}{{AM}} = \frac{{AO}}{{AE}} = \frac{4}{5}\).