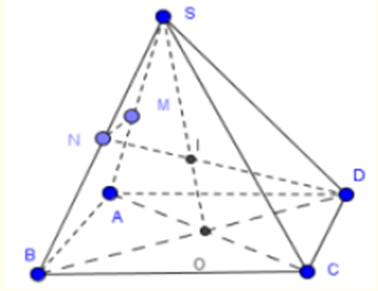
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SB.
a) Tìm giao tuyến của (SAC) và (SBD)
b) Tìm giao điểm DN với (SAC)
c) Chứng minh MN // (SCD).
a) Gọi giao điểm của AC và DB là O
Vì O ∈ AC ⊂ (SAC) nên O ∈ (SAC)
O ∈ BD ⊂ (SBD) nên O ∈ (SBD)
Suy ra O ∈ (SAC) ∩ (SBD)
Mà S ∈ (SAC) ∩ (SBD)
Suy ra SO ∈ (SAC) ∩ (SBD)
b) Gọi I là giao điểm của SO và DN
Ta có:
DN ⊂ (SBD)
SO = (SAC) ∩ (SBD)
Suy ra I = DN ∩ (SAC)
c) Xét tam giác SAB có M, N lần lượt là trung điểm của SA, SB
Suy ra MN là đường trung bình
Do đó MN // AB
Mà AB // CD (vì ABCD là hình bình hành)
Suy ra MN // CD
Lại có CD ⊂ (SCD)
Do đó MN // (SCD)
Vậy MN // (SCD).